Question Number 139950 by I want to learn more last updated on 02/May/21

Answered by TheSupreme last updated on 02/May/21
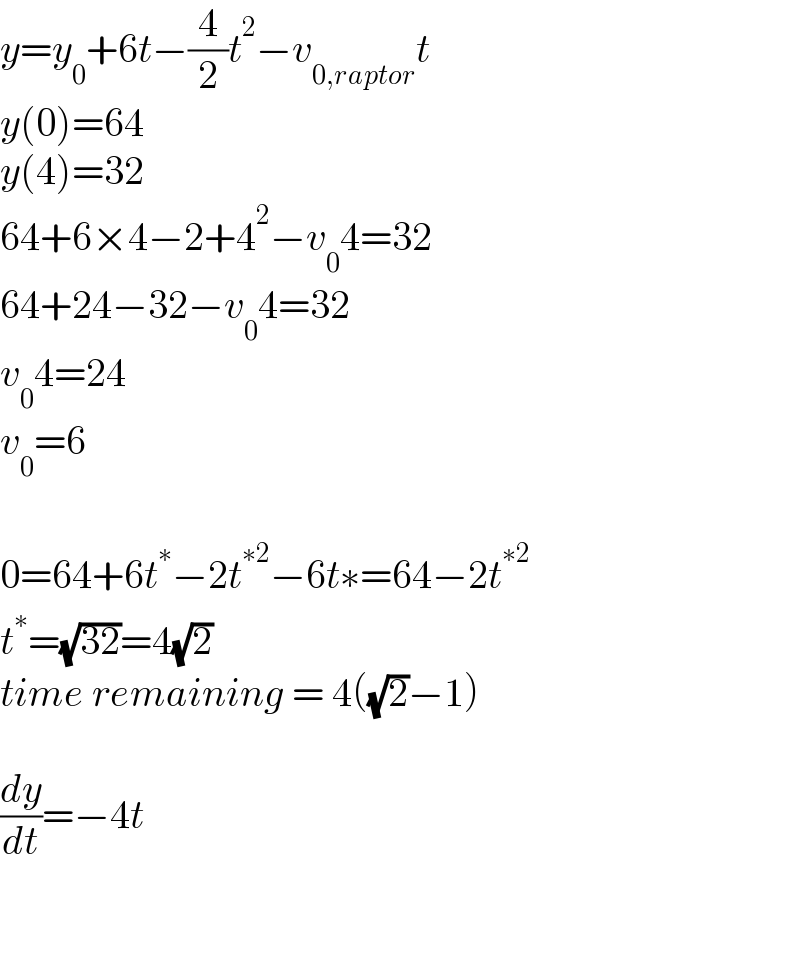
$${y}={y}_{\mathrm{0}} +\mathrm{6}{t}−\frac{\mathrm{4}}{\mathrm{2}}{t}^{\mathrm{2}} −{v}_{\mathrm{0},{raptor}} {t} \\ $$$${y}\left(\mathrm{0}\right)=\mathrm{64} \\ $$$${y}\left(\mathrm{4}\right)=\mathrm{32} \\ $$$$\mathrm{64}+\mathrm{6}×\mathrm{4}−\mathrm{2}+\mathrm{4}^{\mathrm{2}} −{v}_{\mathrm{0}} \mathrm{4}=\mathrm{32} \\ $$$$\mathrm{64}+\mathrm{24}−\mathrm{32}−{v}_{\mathrm{0}} \mathrm{4}=\mathrm{32} \\ $$$${v}_{\mathrm{0}} \mathrm{4}=\mathrm{24} \\ $$$${v}_{\mathrm{0}} =\mathrm{6} \\ $$$$ \\ $$$$\mathrm{0}=\mathrm{64}+\mathrm{6}{t}^{\ast} −\mathrm{2}{t}^{\ast\mathrm{2}} −\mathrm{6}{t}\ast=\mathrm{64}−\mathrm{2}{t}^{\ast\mathrm{2}} \\ $$$${t}^{\ast} =\sqrt{\mathrm{32}}=\mathrm{4}\sqrt{\mathrm{2}} \\ $$$${time}\:{remaining}\:=\:\mathrm{4}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$ \\ $$$$\frac{{dy}}{{dt}}=−\mathrm{4}{t} \\ $$$$ \\ $$$$ \\ $$
Commented by I want to learn more last updated on 02/May/21
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
