Menu Close

Question-139973

Tinku Tara 0 Comments
Pin




Question Number 139973 by ajfour last updated on 02/May/21
Commented by ajfour last updated on 02/May/21
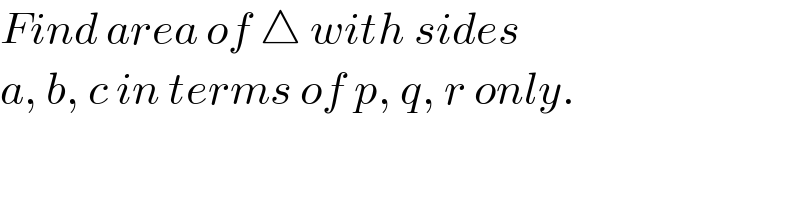
Find area of △ with sides a, b, c in terms of p, q, r only.
$${Find}\:{area}\:{of}\:\bigtriangleup\:{with}\:{sides}\: \\ $$$${a},\:{b},\:{c}\:{in}\:{terms}\:{of}\:{p},\:{q},\:{r}\:{only}. \\ $$
Answered by ajfour last updated on 02/May/21
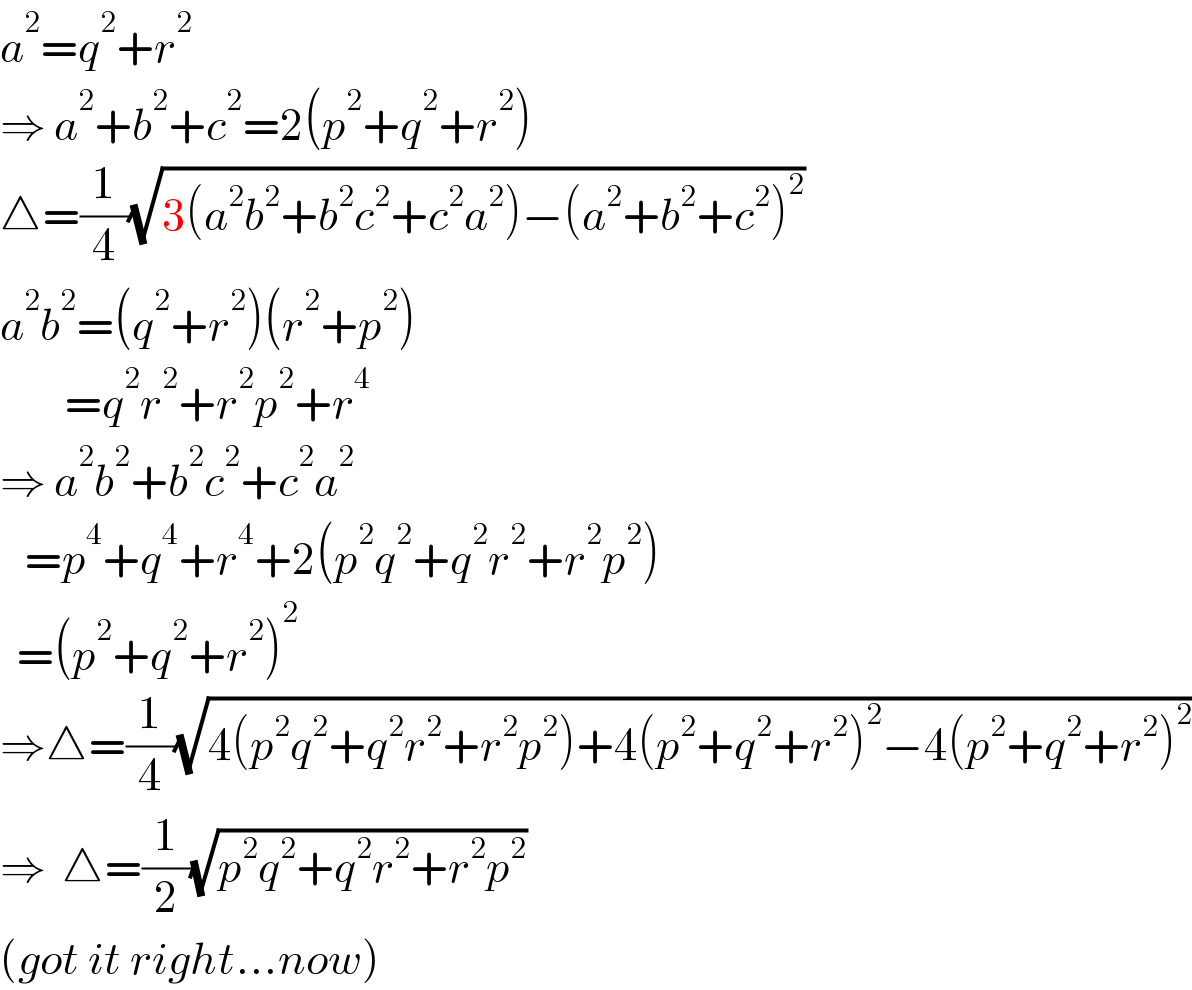
a^2 =q^2 +r^2 ⇒ a^2 +b^2 +c^2 =2(p^2 +q^2 +r^2 ) △=(1/4)(√(3(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^2 +b^2 +c^2 )^2 )) a^2 b^2 =(q^2 +r^2 )(r^2 +p^2 ) =q^2 r^2 +r^2 p^2 +r^4 ⇒ a^2 b^2 +b^2 c^2 +c^2 a^2 =p^4 +q^4 +r^4 +2(p^2 q^2 +q^2 r^2 +r^2 p^2 ) =(p^2 +q^2 +r^2 )^2 ⇒△=(1/4)(√(4(p^2 q^2 +q^2 r^2 +r^2 p^2 )+4(p^2 +q^2 +r^2 )^2 −4(p^2 +q^2 +r^2 )^2 )) ⇒ △=(1/2)(√(p^2 q^2 +q^2 r^2 +r^2 p^2 )) (got it right...now)
$${a}^{\mathrm{2}} ={q}^{\mathrm{2}} +{r}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{3}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} =\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:={q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} +{r}^{\mathrm{4}} \\ $$$$\Rightarrow\:{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \\ $$$$\:\:\:={p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} +\mathrm{2}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right) \\ $$$$\:\:=\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{4}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right)+\mathrm{4}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$$\left({got}\:{it}\:{right}…{now}\right) \\ $$
Commented by ajfour last updated on 02/May/21
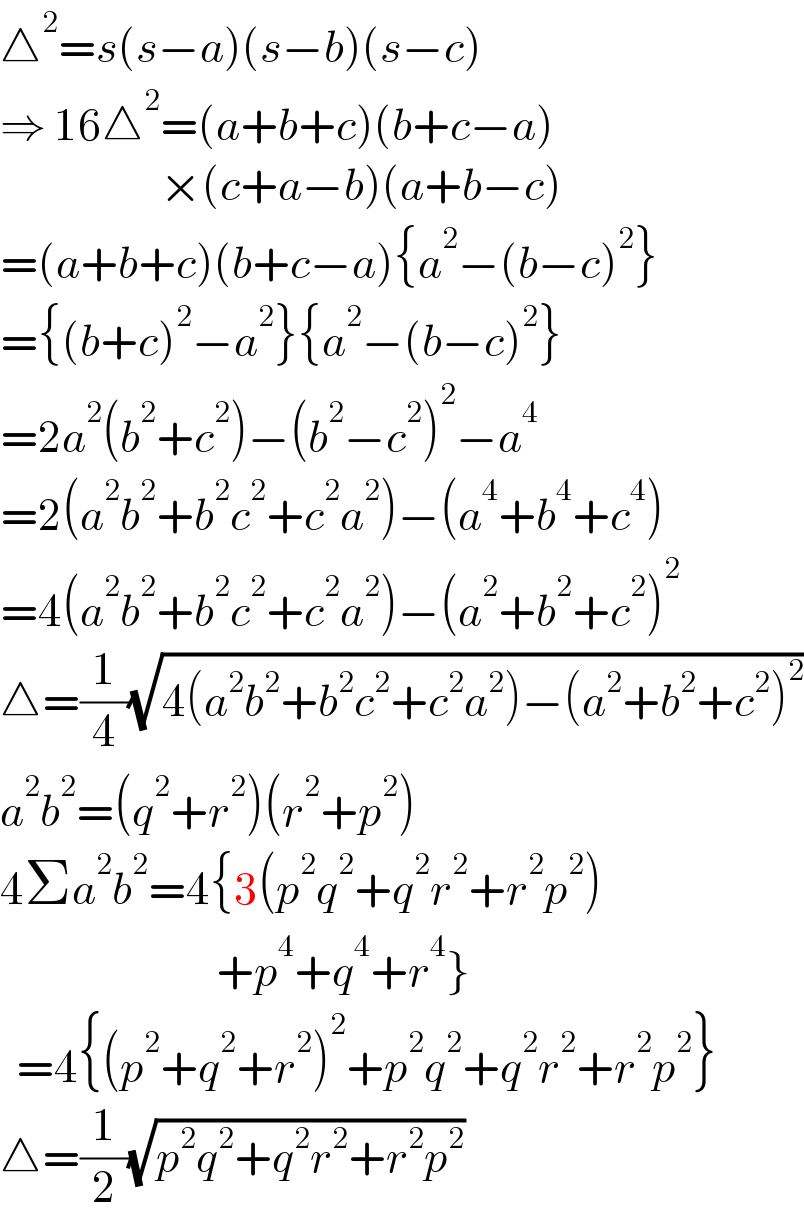
△^2 =s(s−a)(s−b)(s−c) ⇒ 16△^2 =(a+b+c)(b+c−a) ×(c+a−b)(a+b−c) =(a+b+c)(b+c−a){a^2 −(b−c)^2 } ={(b+c)^2 −a^2 }{a^2 −(b−c)^2 } =2a^2 (b^2 +c^2 )−(b^2 −c^2 )^2 −a^4 =2(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^4 +b^4 +c^4 ) =4(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^2 +b^2 +c^2 )^2 △=(1/4)(√(4(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^2 +b^2 +c^2 )^2 )) a^2 b^2 =(q^2 +r^2 )(r^2 +p^2 ) 4Σa^2 b^2 =4{3(p^2 q^2 +q^2 r^2 +r^2 p^2 ) +p^4 +q^4 +r^4 } =4{(p^2 +q^2 +r^2 )^2 +p^2 q^2 +q^2 r^2 +r^2 p^2 } △=(1/2)(√(p^2 q^2 +q^2 r^2 +r^2 p^2 ))
$$\bigtriangleup^{\mathrm{2}} ={s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right) \\ $$$$\Rightarrow\:\mathrm{16}\bigtriangleup^{\mathrm{2}} =\left({a}+{b}+{c}\right)\left({b}+{c}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left({c}+{a}−{b}\right)\left({a}+{b}−{c}\right) \\ $$$$=\left({a}+{b}+{c}\right)\left({b}+{c}−{a}\right)\left\{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right\} \\ $$$$=\left\{\left({b}+{c}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right\}\left\{{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right\} \\ $$$$=\mathrm{2}{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} −{a}^{\mathrm{4}} \\ $$$$=\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right) \\ $$$$=\mathrm{4}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{4}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} =\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}\Sigma{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{4}\left\{\mathrm{3}\left({p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{p}^{\mathrm{4}} +{q}^{\mathrm{4}} +{r}^{\mathrm{4}} \right\} \\ $$$$\:\:=\mathrm{4}\left\{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)^{\mathrm{2}} +{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} \right\} \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$
Answered by mr W last updated on 02/May/21
Commented by mr W last updated on 02/May/21
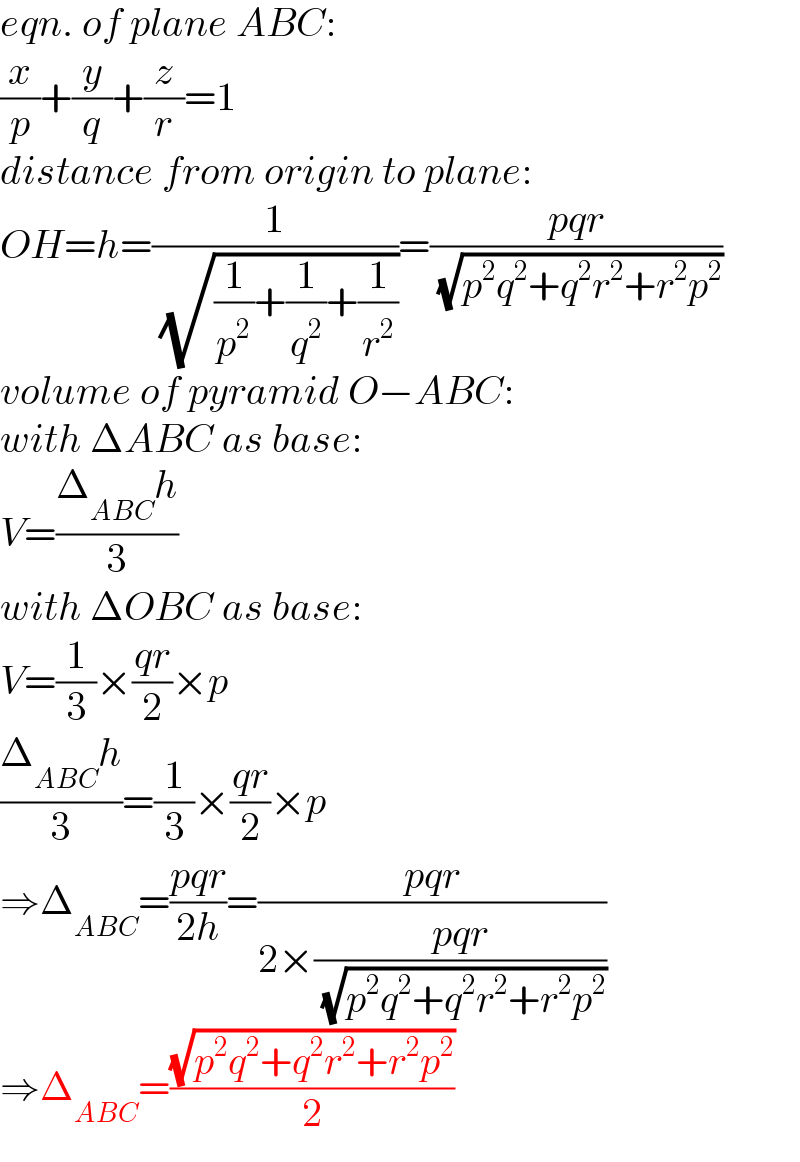
eqn. of plane ABC: (x/p)+(y/q)+(z/r)=1 distance from origin to plane: OH=h=(1/( (√((1/p^2 )+(1/q^2 )+(1/r^2 )))))=((pqr)/( (√(p^2 q^2 +q^2 r^2 +r^2 p^2 )))) volume of pyramid O−ABC: with ΔABC as base: V=((Δ_(ABC) h)/3) with ΔOBC as base: V=(1/3)×((qr)/2)×p ((Δ_(ABC) h)/3)=(1/3)×((qr)/2)×p ⇒Δ_(ABC) =((pqr)/(2h))=((pqr)/(2×((pqr)/( (√(p^2 q^2 +q^2 r^2 +r^2 p^2 )))))) ⇒Δ_(ABC) =((√(p^2 q^2 +q^2 r^2 +r^2 p^2 ))/2)
$${eqn}.\:{of}\:{plane}\:{ABC}: \\ $$$$\frac{{x}}{{p}}+\frac{{y}}{{q}}+\frac{{z}}{{r}}=\mathrm{1} \\ $$$${distance}\:{from}\:{origin}\:{to}\:{plane}: \\ $$$${OH}={h}=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{q}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }}}=\frac{{pqr}}{\:\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }} \\ $$$${volume}\:{of}\:{pyramid}\:{O}−{ABC}: \\ $$$${with}\:\Delta{ABC}\:{as}\:{base}: \\ $$$${V}=\frac{\Delta_{{ABC}} {h}}{\mathrm{3}} \\ $$$${with}\:\Delta{OBC}\:{as}\:{base}: \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{{qr}}{\mathrm{2}}×{p} \\ $$$$\frac{\Delta_{{ABC}} {h}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{{qr}}{\mathrm{2}}×{p} \\ $$$$\Rightarrow\Delta_{{ABC}} =\frac{{pqr}}{\mathrm{2}{h}}=\frac{{pqr}}{\mathrm{2}×\frac{{pqr}}{\:\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }}} \\ $$$$\Rightarrow\Delta_{{ABC}} =\frac{\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} }}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 02/May/21
Thanks Sir!
Commented by ajfour last updated on 21/May/21
what's the expression for circumradius of ∆ABC in terms of p, q, r Sir ?
Answered by ajfour last updated on 02/May/21
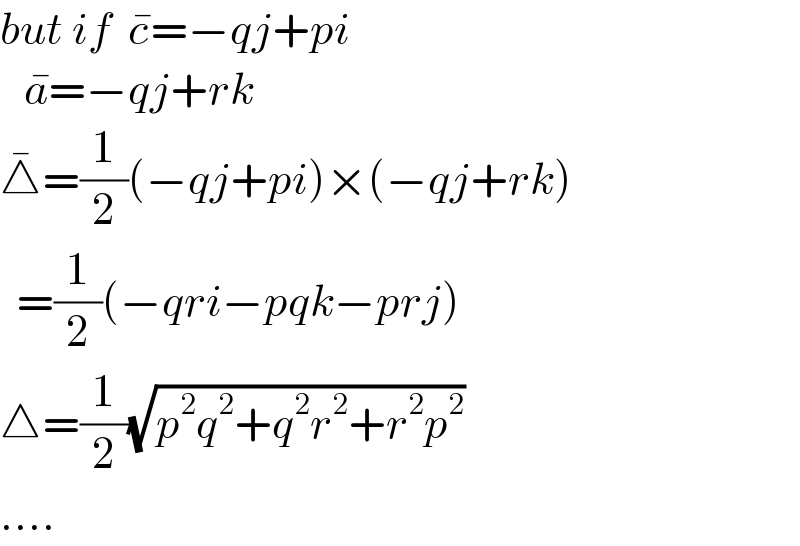
but if c^� =−qj+pi a^� =−qj+rk △^� =(1/2)(−qj+pi)×(−qj+rk) =(1/2)(−qri−pqk−prj) △=(1/2)(√(p^2 q^2 +q^2 r^2 +r^2 p^2 )) ....
$${but}\:{if}\:\:\bar {{c}}=−{qj}+{pi} \\ $$$$\:\:\:\bar {{a}}=−{qj}+{rk} \\ $$$$\bar {\bigtriangleup}=\frac{\mathrm{1}}{\mathrm{2}}\left(−{qj}+{pi}\right)×\left(−{qj}+{rk}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(−{qri}−{pqk}−{prj}\right) \\ $$$$\bigtriangleup=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} {q}^{\mathrm{2}} +{q}^{\mathrm{2}} {r}^{\mathrm{2}} +{r}^{\mathrm{2}} {p}^{\mathrm{2}} } \\ $$$$…. \\ $$
Commented by mr W last updated on 02/May/21
vector way is best!
$${vector}\:{way}\:{is}\:{best}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *