Menu Close

Question-139992

Tinku Tara 0 Comments
Pin




Question Number 139992 by ajfour last updated on 02/May/21
Commented by ajfour last updated on 03/May/21
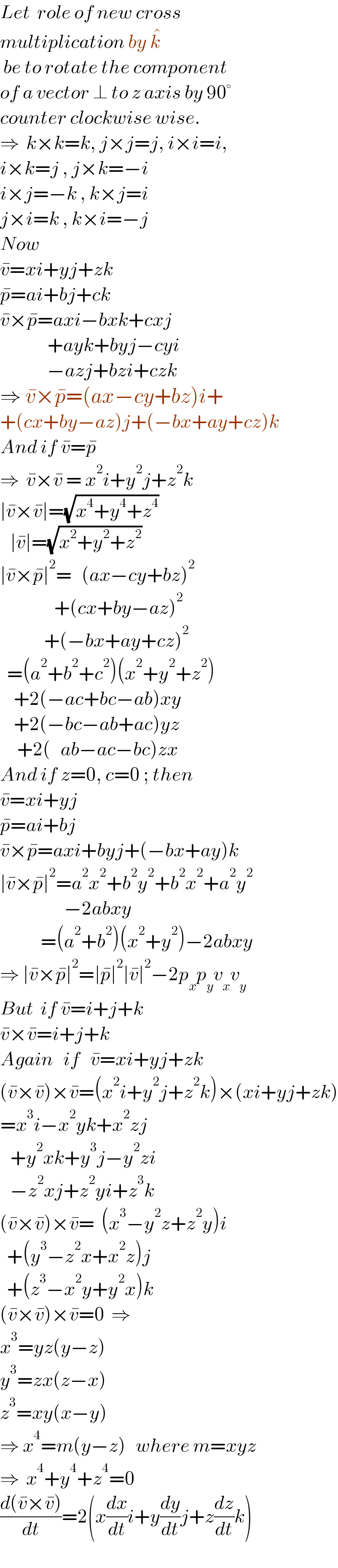
Let role of new cross multiplication by k^� be to rotate the component of a vector ⊥ to z axis by 90° counter clockwise wise. ⇒ k×k=k, j×j=j, i×i=i, i×k=j , j×k=−i i×j=−k , k×j=i j×i=k , k×i=−j Now v^� =xi+yj+zk p^� =ai+bj+ck v^� ×p^� =axi−bxk+cxj +ayk+byj−cyi −azj+bzi+czk ⇒ v^� ×p^� =(ax−cy+bz)i+ +(cx+by−az)j+(−bx+ay+cz)k And if v^� =p^� ⇒ v^� ×v^� = x^2 i+y^2 j+z^2 k ∣v^� ×v^� ∣=(√(x^4 +y^4 +z^4 )) ∣v^� ∣=(√(x^2 +y^2 +z^2 )) ∣v^� ×p^� ∣^2 = (ax−cy+bz)^2 +(cx+by−az)^2 +(−bx+ay+cz)^2 =(a^2 +b^2 +c^2 )(x^2 +y^2 +z^2 ) +2(−ac+bc−ab)xy +2(−bc−ab+ac)yz +2( ab−ac−bc)zx And if z=0, c=0 ; then v^� =xi+yj p^� =ai+bj v^� ×p^� =axi+byj+(−bx+ay)k ∣v^� ×p^� ∣^2 =a^2 x^2 +b^2 y^2 +b^2 x^2 +a^2 y^2 −2abxy =(a^2 +b^2 )(x^2 +y^2 )−2abxy ⇒ ∣v^� ×p^� ∣^2 =∣p^� ∣^2 ∣v^� ∣^2 −2p_x p_y v_x v_y But if v^� =i+j+k v^� ×v^� =i+j+k Again if v^� =xi+yj+zk (v^� ×v^� )×v^� =(x^2 i+y^2 j+z^2 k)×(xi+yj+zk) =x^3 i−x^2 yk+x^2 zj +y^2 xk+y^3 j−y^2 zi −z^2 xj+z^2 yi+z^3 k (v^� ×v^� )×v^� = (x^3 −y^2 z+z^2 y)i +(y^3 −z^2 x+x^2 z)j +(z^3 −x^2 y+y^2 x)k (v^� ×v^� )×v^� =0 ⇒ x^3 =yz(y−z) y^3 =zx(z−x) z^3 =xy(x−y) ⇒ x^4 =m(y−z) where m=xyz ⇒ x^4 +y^4 +z^4 =0 ((d(v^� ×v^� ))/dt)=2(x(dx/dt)i+y(dy/dt)j+z(dz/dt)k)
$${Let}\:\:{role}\:{of}\:{new}\:{cross}\: \\ $$$${multiplication}\:{by}\:\hat {{k}} \\ $$$$\:{be}\:{to}\:{rotate}\:{the}\:{component} \\ $$$${of}\:{a}\:{vector}\:\bot\:{to}\:{z}\:{axis}\:{by}\:\mathrm{90}° \\ $$$${counter}\:{clockwise}\:{wise}. \\ $$$$\Rightarrow\:\:{k}×{k}={k},\:{j}×{j}={j},\:{i}×{i}={i}, \\ $$$${i}×{k}={j}\:,\:{j}×{k}=−{i} \\ $$$${i}×{j}=−{k}\:,\:{k}×{j}={i} \\ $$$${j}×{i}={k}\:,\:{k}×{i}=−{j} \\ $$$${Now} \\ $$$$\bar {{v}}={xi}+{yj}+{zk} \\ $$$$\bar {{p}}={ai}+{bj}+{ck} \\ $$$$\bar {{v}}×\bar {{p}}={axi}−{bxk}+{cxj} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{ayk}+{byj}−{cyi} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{azj}+{bzi}+{czk} \\ $$$$\Rightarrow\:\bar {{v}}×\bar {{p}}=\left({ax}−{cy}+{bz}\right){i}+ \\ $$$$+\left({cx}+{by}−{az}\right){j}+\left(−{bx}+{ay}+{cz}\right){k} \\ $$$${And}\:{if}\:\bar {{v}}=\bar {{p}} \\ $$$$\Rightarrow\:\:\bar {{v}}×\bar {{v}}\:=\:{x}^{\mathrm{2}} {i}+{y}^{\mathrm{2}} {j}+{z}^{\mathrm{2}} {k} \\ $$$$\mid\bar {{v}}×\bar {{v}}\mid=\sqrt{{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} } \\ $$$$\:\:\:\mid\bar {{v}}\mid=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$$\mid\bar {{v}}×\bar {{p}}\mid^{\mathrm{2}} =\:\:\:\left({ax}−{cy}+{bz}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({cx}+{by}−{az}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(−{bx}+{ay}+{cz}\right)^{\mathrm{2}} \\ $$$$\:\:=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:+\mathrm{2}\left(−{ac}+{bc}−{ab}\right){xy} \\ $$$$\:\:\:\:+\mathrm{2}\left(−{bc}−{ab}+{ac}\right){yz} \\ $$$$\:\:\:\:\:+\mathrm{2}\left(\:\:\:{ab}−{ac}−{bc}\right){zx} \\ $$$${And}\:{if}\:{z}=\mathrm{0},\:{c}=\mathrm{0}\:;\:{then} \\ $$$$\bar {{v}}={xi}+{yj} \\ $$$$\bar {{p}}={ai}+{bj} \\ $$$$\bar {{v}}×\bar {{p}}={axi}+{byj}+\left(−{bx}+{ay}\right){k} \\ $$$$\mid\bar {{v}}×\bar {{p}}\mid^{\mathrm{2}} ={a}^{\mathrm{2}} {x}^{\mathrm{2}} +{b}^{\mathrm{2}} {y}^{\mathrm{2}} +{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}{abxy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{abxy} \\ $$$$\Rightarrow\:\mid\bar {{v}}×\bar {{p}}\mid^{\mathrm{2}} =\mid\bar {{p}}\mid^{\mathrm{2}} \mid\bar {{v}}\mid^{\mathrm{2}} −\mathrm{2}{p}_{{x}} {p}_{{y}} {v}_{{x}} {v}_{{y}} \\ $$$${But}\:\:{if}\:\bar {{v}}={i}+{j}+{k} \\ $$$$\bar {{v}}×\bar {{v}}={i}+{j}+{k} \\ $$$${Again}\:\:\:{if}\:\:\:\bar {{v}}={xi}+{yj}+{zk} \\ $$$$\left(\bar {{v}}×\bar {{v}}\right)×\bar {{v}}=\left({x}^{\mathrm{2}} {i}+{y}^{\mathrm{2}} {j}+{z}^{\mathrm{2}} {k}\right)×\left({xi}+{yj}+{zk}\right) \\ $$$$={x}^{\mathrm{3}} {i}−{x}^{\mathrm{2}} {yk}+{x}^{\mathrm{2}} {zj} \\ $$$$\:\:\:+{y}^{\mathrm{2}} {xk}+{y}^{\mathrm{3}} {j}−{y}^{\mathrm{2}} {zi} \\ $$$$\:\:\:−{z}^{\mathrm{2}} {xj}+{z}^{\mathrm{2}} {yi}+{z}^{\mathrm{3}} {k} \\ $$$$\left(\bar {{v}}×\bar {{v}}\right)×\bar {{v}}=\:\:\left({x}^{\mathrm{3}} −{y}^{\mathrm{2}} {z}+{z}^{\mathrm{2}} {y}\right){i} \\ $$$$\:\:+\left({y}^{\mathrm{3}} −{z}^{\mathrm{2}} {x}+{x}^{\mathrm{2}} {z}\right){j} \\ $$$$\:\:+\left({z}^{\mathrm{3}} −{x}^{\mathrm{2}} {y}+{y}^{\mathrm{2}} {x}\right){k} \\ $$$$\left(\bar {{v}}×\bar {{v}}\right)×\bar {{v}}=\mathrm{0}\:\:\Rightarrow \\ $$$${x}^{\mathrm{3}} ={yz}\left({y}−{z}\right) \\ $$$${y}^{\mathrm{3}} ={zx}\left({z}−{x}\right) \\ $$$${z}^{\mathrm{3}} ={xy}\left({x}−{y}\right) \\ $$$$\Rightarrow\:{x}^{\mathrm{4}} ={m}\left({y}−{z}\right)\:\:\:{where}\:{m}={xyz} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{4}} +{y}^{\mathrm{4}} +{z}^{\mathrm{4}} =\mathrm{0} \\ $$$$\frac{{d}\left(\bar {{v}}×\bar {{v}}\right)}{{dt}}=\mathrm{2}\left({x}\frac{{dx}}{{dt}}{i}+{y}\frac{{dy}}{{dt}}{j}+{z}\frac{{dz}}{{dt}}{k}\right) \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *