Question-140207

Question Number 140207 by mathlove last updated on 05/May/21

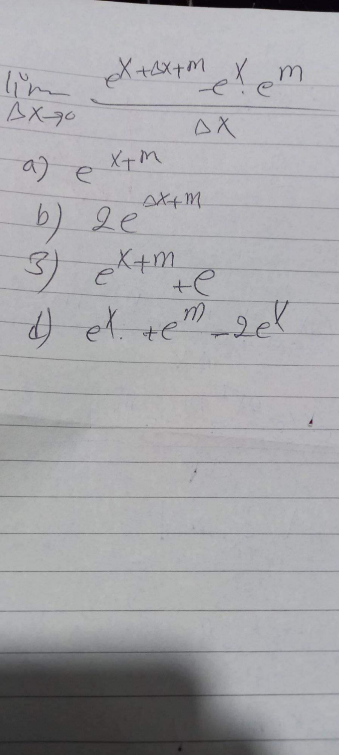
Answered by liberty last updated on 06/May/21

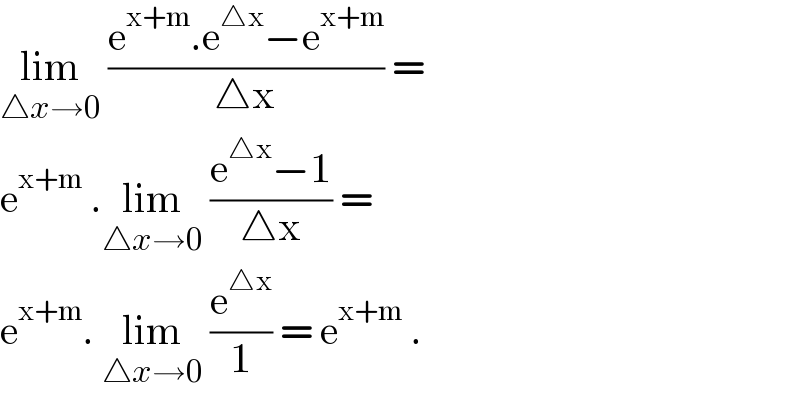
lim_(△x→0) ((e^(x+m) .e^(△x) −e^(x+m) )/(△x)) = e^(x+m) .lim_(△x→0) ((e^(△x) −1)/(△x)) = e^(x+m) . lim_(△x→0) (e^(△x) /1) = e^(x+m) .

$$\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\mathrm{x}+\mathrm{m}} .\mathrm{e}^{\bigtriangleup\mathrm{x}} −\mathrm{e}^{\mathrm{x}+\mathrm{m}} }{\bigtriangleup\mathrm{x}}\:= \\ $$$$\mathrm{e}^{\mathrm{x}+\mathrm{m}} \:.\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\bigtriangleup\mathrm{x}} −\mathrm{1}}{\bigtriangleup\mathrm{x}}\:= \\ $$$$\mathrm{e}^{\mathrm{x}+\mathrm{m}} .\:\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\bigtriangleup\mathrm{x}} }{\mathrm{1}}\:=\:\mathrm{e}^{\mathrm{x}+\mathrm{m}} \:. \\ $$

Answered by wassim last updated on 05/May/21

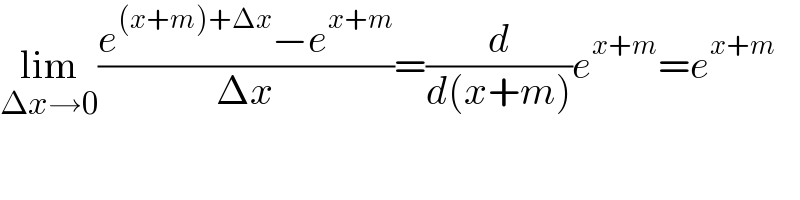
lim_(Δx→0) ((e^((x+m)+Δx) −e^(x+m) )/(Δx))=(d/(d(x+m)))e^(x+m) =e^(x+m)

$$\underset{\Delta{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\left({x}+{m}\right)+\Delta{x}} −{e}^{{x}+{m}} }{\Delta{x}}=\frac{{d}}{{d}\left({x}+{m}\right)}{e}^{{x}+{m}} ={e}^{{x}+{m}} \\ $$

Facebook Tweet Pin

Question-140207

Leave a Reply Cancel reply