Question Number 140698 by BHOOPENDRA last updated on 11/May/21

Commented by BHOOPENDRA last updated on 11/May/21

$${B}\:{part}\:{Mr}.{W}\: \\ $$
Answered by mr W last updated on 11/May/21
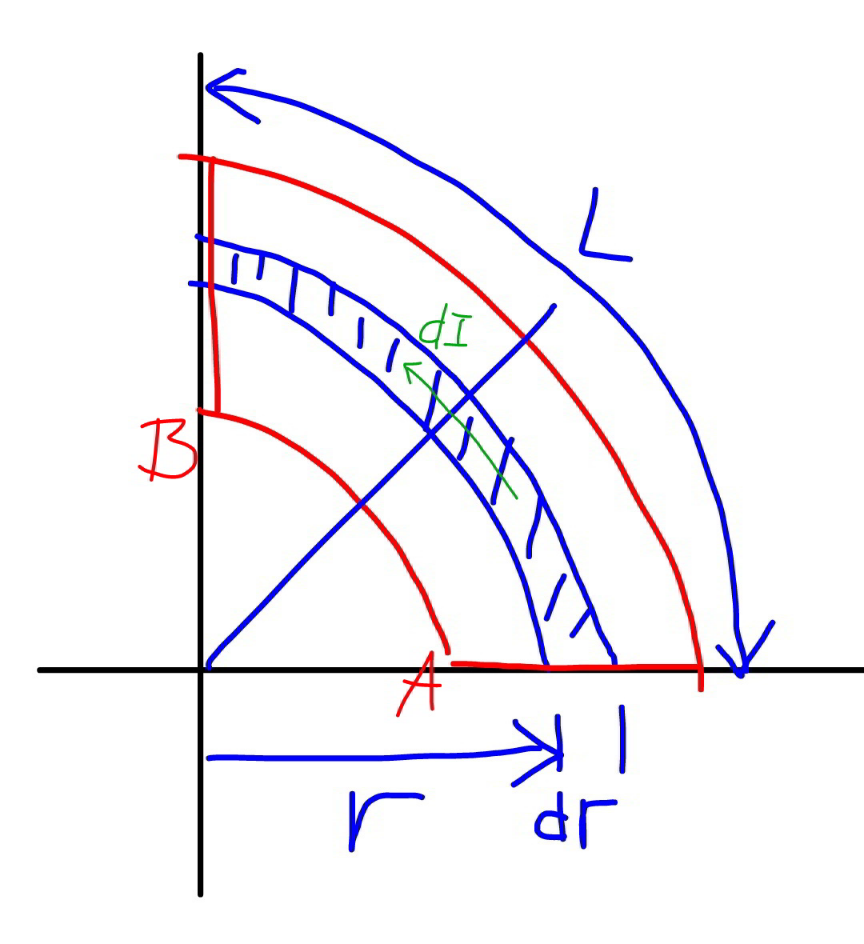
Commented by mr W last updated on 11/May/21
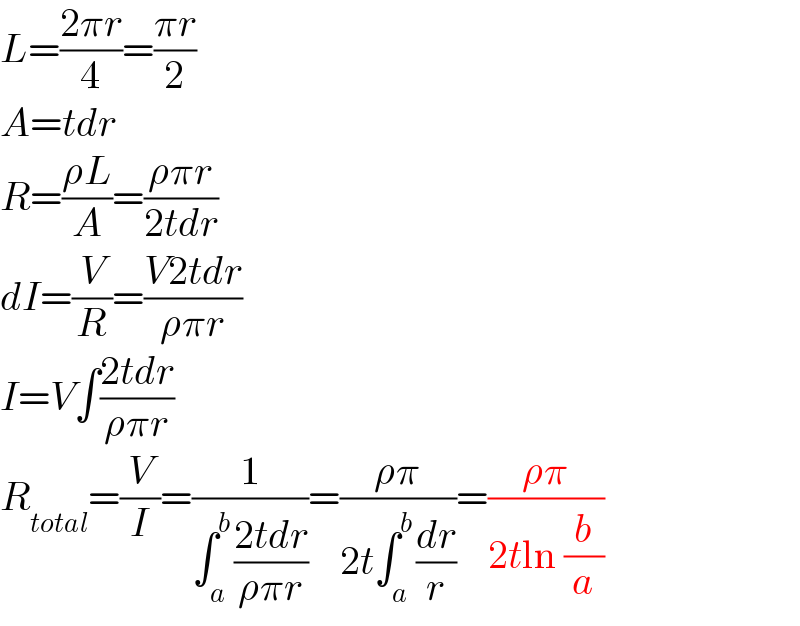
$${L}=\frac{\mathrm{2}\pi{r}}{\mathrm{4}}=\frac{\pi{r}}{\mathrm{2}} \\ $$$${A}={tdr} \\ $$$${R}=\frac{\rho{L}}{{A}}=\frac{\rho\pi{r}}{\mathrm{2}{tdr}} \\ $$$${dI}=\frac{{V}}{{R}}=\frac{{V}\mathrm{2}{tdr}}{\rho\pi{r}} \\ $$$${I}={V}\int\frac{\mathrm{2}{tdr}}{\rho\pi{r}} \\ $$$${R}_{{total}} =\frac{{V}}{{I}}=\frac{\mathrm{1}}{\int_{{a}} ^{{b}} \frac{\mathrm{2}{tdr}}{\rho\pi{r}}}=\frac{\rho\pi}{\mathrm{2}{t}\int_{{a}} ^{{b}} \frac{{dr}}{{r}}}=\frac{\rho\pi}{\mathrm{2}{t}\mathrm{ln}\:\frac{{b}}{{a}}} \\ $$
Commented by BHOOPENDRA last updated on 11/May/21

$${thankyou}\: \\ $$
