Menu Close

Question-140703

Tinku Tara 0 Comments
Pin




Question Number 140703 by rs4089 last updated on 11/May/21
Answered by Dwaipayan Shikari last updated on 11/May/21
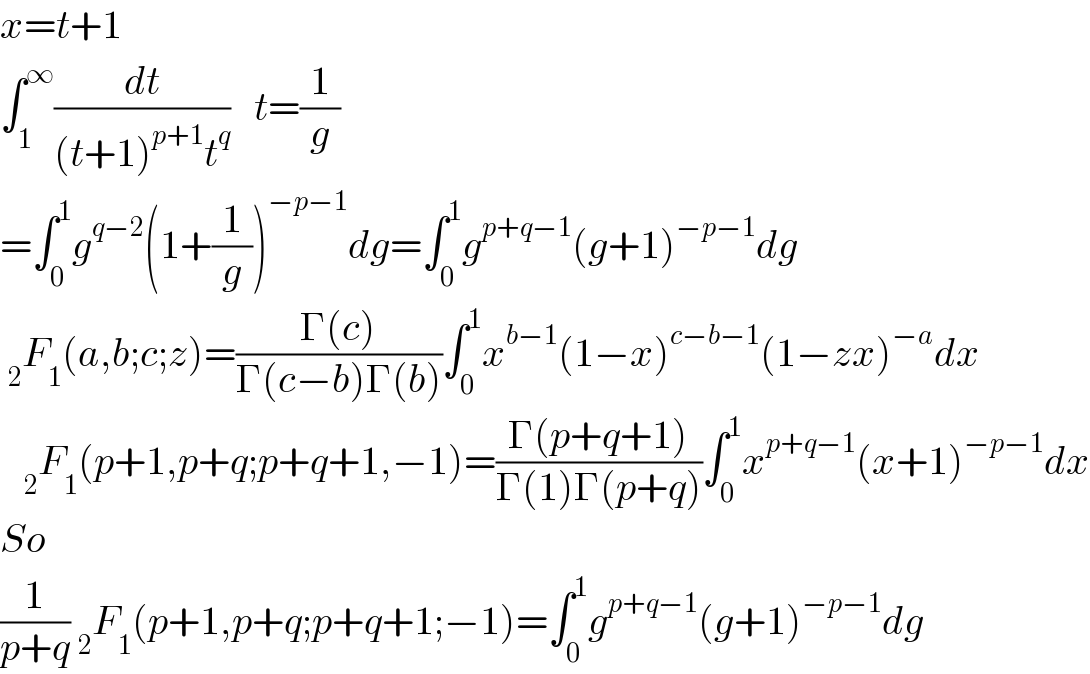
x=t+1 ∫_1 ^∞ (dt/((t+1)^(p+1) t^q )) t=(1/g) =∫_0 ^1 g^(q−2) (1+(1/g))^(−p−1) dg=∫_0 ^1 g^(p+q−1) (g+1)^(−p−1) dg _2 F_1 (a,b;c;z)=((Γ(c))/(Γ(c−b)Γ(b)))∫_0 ^1 x^(b−1) (1−x)^(c−b−1) (1−zx)^(−a) dx _2 F_1 (p+1,p+q;p+q+1,−1)=((Γ(p+q+1))/(Γ(1)Γ(p+q)))∫_0 ^1 x^(p+q−1) (x+1)^(−p−1) dx So (1/(p+q)) _2 F_1 (p+1,p+q;p+q+1;−1)=∫_0 ^1 g^(p+q−1) (g+1)^(−p−1) dg
$${x}={t}+\mathrm{1} \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{\left({t}+\mathrm{1}\right)^{{p}+\mathrm{1}} {t}^{{q}} }\:\:\:{t}=\frac{\mathrm{1}}{{g}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {g}^{{q}−\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{g}}\right)^{−{p}−\mathrm{1}} {dg}=\int_{\mathrm{0}} ^{\mathrm{1}} {g}^{{p}+{q}−\mathrm{1}} \left({g}+\mathrm{1}\right)^{−{p}−\mathrm{1}} {dg} \\ $$$$\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({a},{b};{c};{z}\right)=\frac{\Gamma\left({c}\right)}{\Gamma\left({c}−{b}\right)\Gamma\left({b}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{b}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{c}−{b}−\mathrm{1}} \left(\mathrm{1}−{zx}\right)^{−{a}} {dx} \\ $$$$\:\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({p}+\mathrm{1},{p}+{q};{p}+{q}+\mathrm{1},−\mathrm{1}\right)=\frac{\Gamma\left({p}+{q}+\mathrm{1}\right)}{\Gamma\left(\mathrm{1}\right)\Gamma\left({p}+{q}\right)}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{p}+{q}−\mathrm{1}} \left({x}+\mathrm{1}\right)^{−{p}−\mathrm{1}} {dx} \\ $$$${So} \\ $$$$\frac{\mathrm{1}}{{p}+{q}}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left({p}+\mathrm{1},{p}+{q};{p}+{q}+\mathrm{1};−\mathrm{1}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {g}^{{p}+{q}−\mathrm{1}} \left({g}+\mathrm{1}\right)^{−{p}−\mathrm{1}} {dg} \\ $$
Answered by Mathspace last updated on 12/May/21
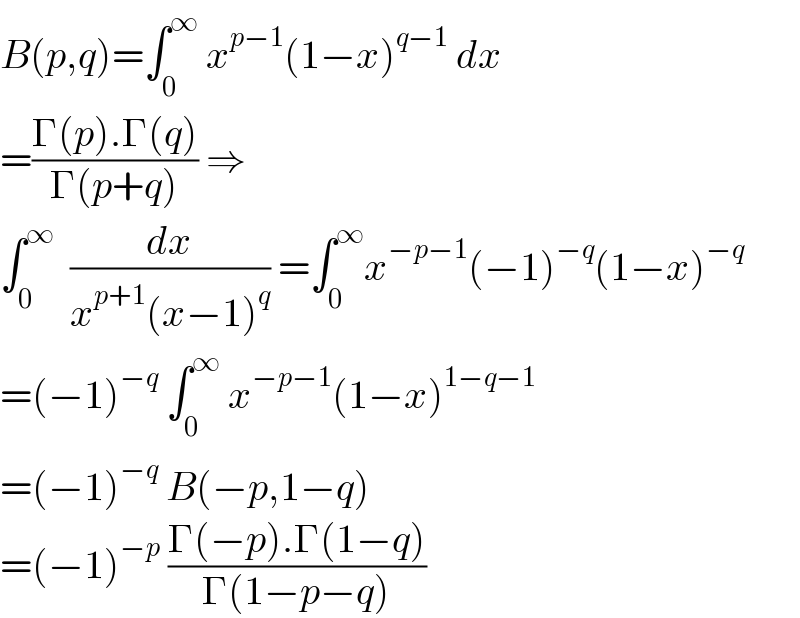
B(p,q)=∫_0 ^∞ x^(p−1) (1−x)^(q−1) dx =((Γ(p).Γ(q))/(Γ(p+q))) ⇒ ∫_0 ^∞ (dx/(x^(p+1) (x−1)^q )) =∫_0 ^∞ x^(−p−1) (−1)^(−q) (1−x)^(−q) =(−1)^(−q) ∫_0 ^∞ x^(−p−1) (1−x)^(1−q−1) =(−1)^(−q) B(−p,1−q) =(−1)^(−p) ((Γ(−p).Γ(1−q))/(Γ(1−p−q)))
$${B}\left({p},{q}\right)=\int_{\mathrm{0}} ^{\infty} \:{x}^{{p}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{q}−\mathrm{1}} \:{dx} \\ $$$$=\frac{\Gamma\left({p}\right).\Gamma\left({q}\right)}{\Gamma\left({p}+{q}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{x}^{{p}+\mathrm{1}} \left({x}−\mathrm{1}\right)^{{q}} }\:=\int_{\mathrm{0}} ^{\infty} {x}^{−{p}−\mathrm{1}} \left(−\mathrm{1}\right)^{−{q}} \left(\mathrm{1}−{x}\right)^{−{q}} \\ $$$$=\left(−\mathrm{1}\right)^{−{q}} \:\int_{\mathrm{0}} ^{\infty} \:{x}^{−{p}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\mathrm{1}−{q}−\mathrm{1}} \\ $$$$=\left(−\mathrm{1}\right)^{−{q}} \:{B}\left(−{p},\mathrm{1}−{q}\right) \\ $$$$=\left(−\mathrm{1}\right)^{−{p}} \:\frac{\Gamma\left(−{p}\right).\Gamma\left(\mathrm{1}−{q}\right)}{\Gamma\left(\mathrm{1}−{p}−{q}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *