Question-140941

Question Number 140941 by mr W last updated on 14/May/21

Commented by mr W last updated on 14/May/21

$${see}\:{Q}\mathrm{140735} \\ $$

Commented by mr W last updated on 14/May/21

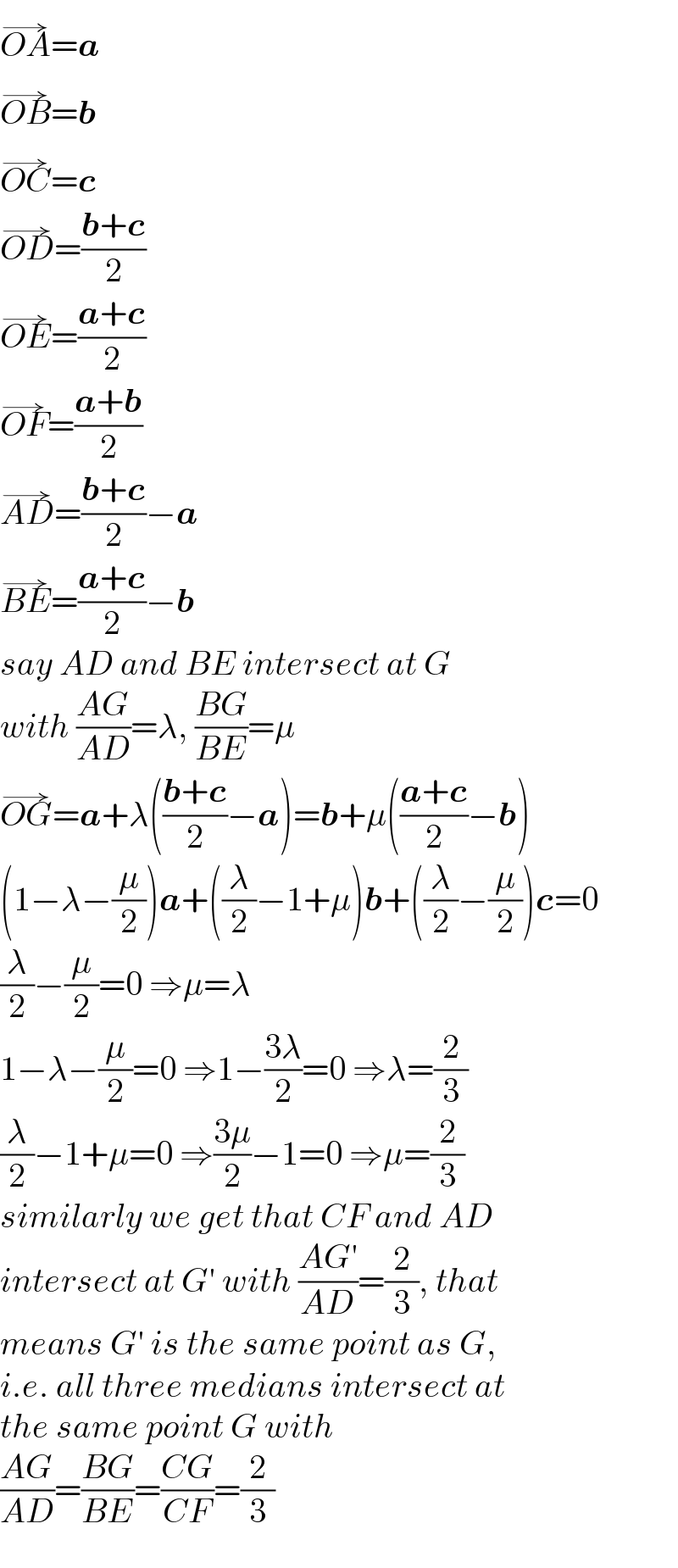
OA^(→) =a OB^(→) =b OC^(→) =c OD^(→) =((b+c)/2) OE^(→) =((a+c)/2) OF^(→) =((a+b)/2) AD^(→) =((b+c)/2)−a BE^(→) =((a+c)/2)−b say AD and BE intersect at G with ((AG)/(AD))=λ, ((BG)/(BE))=μ OG^(→) =a+λ(((b+c)/2)−a)=b+μ(((a+c)/2)−b) (1−λ−(μ/2))a+((λ/2)−1+μ)b+((λ/2)−(μ/2))c=0 (λ/2)−(μ/2)=0 ⇒μ=λ 1−λ−(μ/2)=0 ⇒1−((3λ)/2)=0 ⇒λ=(2/3) (λ/2)−1+μ=0 ⇒((3μ)/2)−1=0 ⇒μ=(2/3) similarly we get that CF and AD intersect at G′ with ((AG′)/(AD))=(2/3), that means G′ is the same point as G, i.e. all three medians intersect at the same point G with ((AG)/(AD))=((BG)/(BE))=((CG)/(CF))=(2/3)

$$\overset{\rightarrow} {{OA}}=\boldsymbol{{a}} \\ $$$$\overset{\rightarrow} {{OB}}=\boldsymbol{{b}} \\ $$$$\overset{\rightarrow} {{OC}}=\boldsymbol{{c}} \\ $$$$\overset{\rightarrow} {{OD}}=\frac{\boldsymbol{{b}}+\boldsymbol{{c}}}{\mathrm{2}} \\ $$$$\overset{\rightarrow} {{OE}}=\frac{\boldsymbol{{a}}+\boldsymbol{{c}}}{\mathrm{2}} \\ $$$$\overset{\rightarrow} {{OF}}=\frac{\boldsymbol{{a}}+\boldsymbol{{b}}}{\mathrm{2}} \\ $$$$\overset{\rightarrow} {{AD}}=\frac{\boldsymbol{{b}}+\boldsymbol{{c}}}{\mathrm{2}}−\boldsymbol{{a}} \\ $$$$\overset{\rightarrow} {{BE}}=\frac{\boldsymbol{{a}}+\boldsymbol{{c}}}{\mathrm{2}}−\boldsymbol{{b}} \\ $$$${say}\:{AD}\:{and}\:{BE}\:{intersect}\:{at}\:{G} \\ $$$${with}\:\frac{{AG}}{{AD}}=\lambda,\:\frac{{BG}}{{BE}}=\mu \\ $$$$\overset{\rightarrow} {{OG}}=\boldsymbol{{a}}+\lambda\left(\frac{\boldsymbol{{b}}+\boldsymbol{{c}}}{\mathrm{2}}−\boldsymbol{{a}}\right)=\boldsymbol{{b}}+\mu\left(\frac{\boldsymbol{{a}}+\boldsymbol{{c}}}{\mathrm{2}}−\boldsymbol{{b}}\right) \\ $$$$\left(\mathrm{1}−\lambda−\frac{\mu}{\mathrm{2}}\right)\boldsymbol{{a}}+\left(\frac{\lambda}{\mathrm{2}}−\mathrm{1}+\mu\right)\boldsymbol{{b}}+\left(\frac{\lambda}{\mathrm{2}}−\frac{\mu}{\mathrm{2}}\right)\boldsymbol{{c}}=\mathrm{0} \\ $$$$\frac{\lambda}{\mathrm{2}}−\frac{\mu}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\mu=\lambda \\ $$$$\mathrm{1}−\lambda−\frac{\mu}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\mathrm{1}−\frac{\mathrm{3}\lambda}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\lambda=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{\lambda}{\mathrm{2}}−\mathrm{1}+\mu=\mathrm{0}\:\Rightarrow\frac{\mathrm{3}\mu}{\mathrm{2}}−\mathrm{1}=\mathrm{0}\:\Rightarrow\mu=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${similarly}\:{we}\:{get}\:{that}\:{CF}\:{and}\:{AD} \\ $$$${intersect}\:{at}\:{G}'\:{with}\:\frac{{AG}'}{{AD}}=\frac{\mathrm{2}}{\mathrm{3}},\:{that} \\ $$$${means}\:{G}'\:{is}\:{the}\:{same}\:{point}\:{as}\:{G}, \\ $$$${i}.{e}.\:{all}\:{three}\:{medians}\:{intersect}\:{at} \\ $$$${the}\:{same}\:{point}\:{G}\:{with} \\ $$$$\frac{{AG}}{{AD}}=\frac{{BG}}{{BE}}=\frac{{CG}}{{CF}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Answered by ajfour last updated on 14/May/21

AB=c^� (let A origin) AC=b^� line CF r=b+λ(c−2b) line AD r= μ(b+c) intersection λ= μ and 1−2λ=μ ⇒ λ=μ=(1/3) ⇒ r_G = ((b+c)/3) line BE r=c+ρ(b−2c) lets check if r_G lies on it ((b+c)/3)=c+ρ(b−2c) ⇒ ρ_1 =(1/3) and ρ_2 =(1/3) hence affirmed.

$${AB}=\bar {{c}}\:\:\:\:\left({let}\:{A}\:{origin}\right) \\ $$$${AC}=\bar {{b}} \\ $$$${line}\:\:{CF}\:\:\:\:\:\:{r}={b}+\lambda\left({c}−\mathrm{2}{b}\right) \\ $$$${line}\:\:{AD}\:\:\:\:\:{r}=\:\mu\left({b}+{c}\right) \\ $$$${intersection} \\ $$$$\:\:\lambda=\:\mu\:\:\:{and}\:\:\mathrm{1}−\mathrm{2}\lambda=\mu \\ $$$$\Rightarrow\:\lambda=\mu=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:{r}_{{G}} =\:\frac{{b}+{c}}{\mathrm{3}} \\ $$$${line}\:{BE}\:\:\:{r}={c}+\rho\left({b}−\mathrm{2}{c}\right) \\ $$$$\:\:\:{lets}\:{check}\:{if}\:{r}_{{G}} \:{lies}\:{on}\:{it} \\ $$$$\:\:\:\frac{{b}+{c}}{\mathrm{3}}={c}+\rho\left({b}−\mathrm{2}{c}\right) \\ $$$$\Rightarrow\:\:\:\rho_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\:\:\:{and}\:\:\rho_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\:\:{hence}\:\:{affirmed}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply