Question Number 141050 by mathsuji last updated on 15/May/21
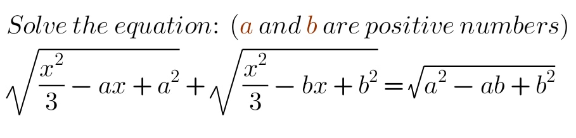
Answered by MJS_new last updated on 15/May/21
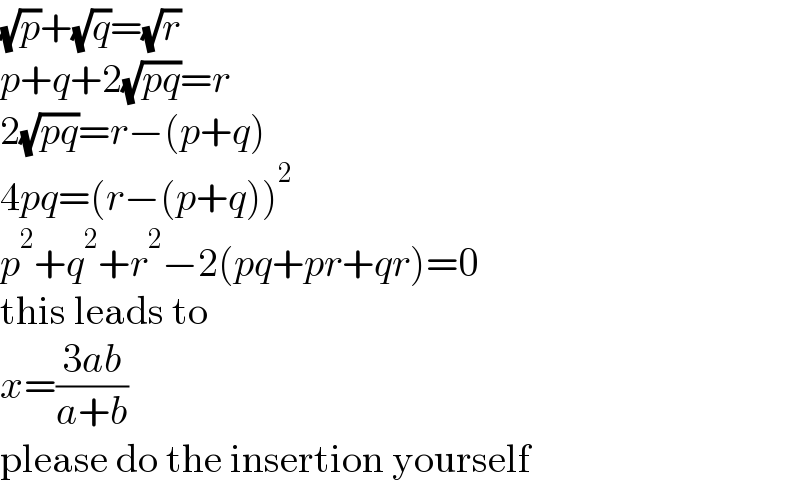
$$\sqrt{{p}}+\sqrt{{q}}=\sqrt{{r}} \\ $$$${p}+{q}+\mathrm{2}\sqrt{{pq}}={r} \\ $$$$\mathrm{2}\sqrt{{pq}}={r}−\left({p}+{q}\right) \\ $$$$\mathrm{4}{pq}=\left({r}−\left({p}+{q}\right)\right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}\left({pq}+{pr}+{qr}\right)=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}=\frac{\mathrm{3}{ab}}{{a}+{b}} \\ $$$$\mathrm{please}\:\mathrm{do}\:\mathrm{the}\:\mathrm{insertion}\:\mathrm{yourself} \\ $$
Commented by mathsuji last updated on 15/May/21
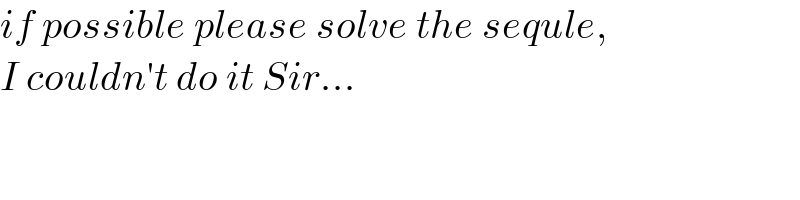
$${if}\:{possible}\:{please}\:{solve}\:{the}\:{sequle}, \\ $$$${I}\:{couldn}'{t}\:{do}\:{it}\:{Sir}… \\ $$
Commented by mathsuji last updated on 15/May/21
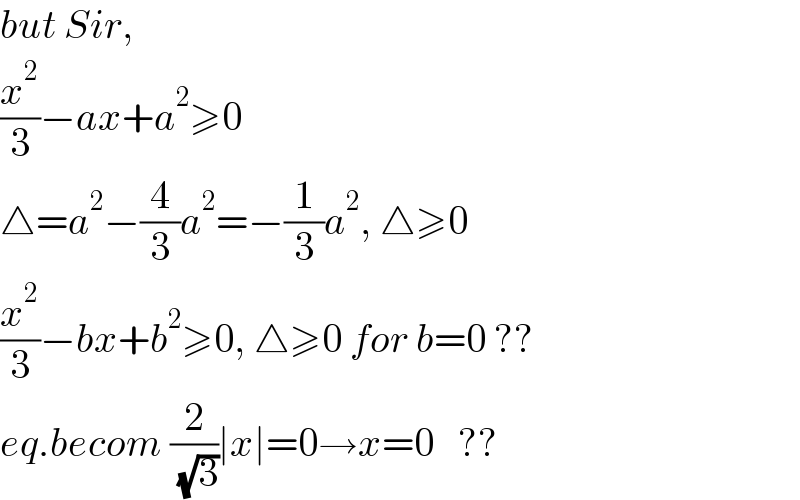
$${but}\:{Sir}, \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{ax}+{a}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\bigtriangleup={a}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{a}^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{3}}{a}^{\mathrm{2}} ,\:\bigtriangleup\geqslant\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{bx}+{b}^{\mathrm{2}} \geqslant\mathrm{0},\:\bigtriangleup\geqslant\mathrm{0}\:{for}\:{b}=\mathrm{0}\:?? \\ $$$${eq}.{becom}\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mid{x}\mid=\mathrm{0}\rightarrow{x}=\mathrm{0}\:\:\:?? \\ $$
Commented by MJS_new last updated on 15/May/21
![where′s the problem? • 1 a, b positive ⇔ a>0∧b>0 • 2 f(x)=(x^2 /3)−Cx+C^2 f ′(x)=0 (2/3)x−C=0 ⇒ x=((3C)/2) minimum of f(x) = f(((3C)/2))=(C^2 /4)>0∀C>0 • 3 a^2 −ab+b^2 =(a−b)^2 +ab>0∀a, b >0 • 4 [insertion] p^2 +q^2 +r^2 −2(pq+pr+qr)=0 p=(x^2 /3)−ax+a^2 q=(x^2 /3)−bx+b^2 r=a^2 −ab+b^2 this leads to −(1/3)(a+b)^2 x^2 +2ab(a+b)x−3a^2 b^2 =0 x^2 −((6ab)/(a+b))x+((9a^2 b^2 )/((a+b)^2 ))=0 (x−((3ab)/(a+b)))^2 =0 x=((3ab)/(a+b)) • 5 [test] (√((x^2 /3)−ax+a^2 ))=(√((((3ab)^2 )/(3(a+b)^2 ))−((3a^2 b)/(a+b))+a^2 ))= =(√((a^2 /((a+b)^2 ))(a^2 −ab+b^2 )))=(a/(a+b))(√(a^2 −ab+b^2 )) similar (√((x^2 /3)−bx+b^2 ))=(b/(a+b))(√(a^2 −ab+b^2 )) and (a/(a+b))(√(a^2 −ab+b^2 ))+(b/(a+b))(√(a^2 −ab+b^2 ))= =((a+b)/(a+b))(√(a^2 −ab+b^2 ))=(√(a^2 −ab+b^2 ))](https://www.tinkutara.com/question/Q141105.png)
$$\mathrm{where}'\mathrm{s}\:\mathrm{the}\:\mathrm{problem}? \\ $$$$\bullet\:\mathrm{1} \\ $$$${a},\:{b}\:\mathrm{positive}\:\Leftrightarrow\:{a}>\mathrm{0}\wedge{b}>\mathrm{0} \\ $$$$\bullet\:\mathrm{2} \\ $$$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{Cx}+{C}^{\mathrm{2}} \\ $$$${f}\:'\left({x}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{x}−{C}=\mathrm{0}\:\Rightarrow\:{x}=\frac{\mathrm{3}{C}}{\mathrm{2}} \\ $$$$\mathrm{minimum}\:\mathrm{of}\:{f}\left({x}\right)\:=\:{f}\left(\frac{\mathrm{3}{C}}{\mathrm{2}}\right)=\frac{{C}^{\mathrm{2}} }{\mathrm{4}}>\mathrm{0}\forall{C}>\mathrm{0} \\ $$$$\bullet\:\mathrm{3} \\ $$$${a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} =\left({a}−{b}\right)^{\mathrm{2}} +{ab}>\mathrm{0}\forall{a},\:{b}\:>\mathrm{0} \\ $$$$\bullet\:\mathrm{4}\:\left[\mathrm{insertion}\right] \\ $$$${p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}\left({pq}+{pr}+{qr}\right)=\mathrm{0} \\ $$$${p}=\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{ax}+{a}^{\mathrm{2}} \\ $$$${q}=\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{bx}+{b}^{\mathrm{2}} \\ $$$${r}={a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \\ $$$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to} \\ $$$$−\frac{\mathrm{1}}{\mathrm{3}}\left({a}+{b}\right)^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{2}{ab}\left({a}+{b}\right){x}−\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{6}{ab}}{{a}+{b}}{x}+\frac{\mathrm{9}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left({x}−\frac{\mathrm{3}{ab}}{{a}+{b}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{\mathrm{3}{ab}}{{a}+{b}} \\ $$$$\bullet\:\mathrm{5}\:\left[\mathrm{test}\right] \\ $$$$\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{ax}+{a}^{\mathrm{2}} }=\sqrt{\frac{\left(\mathrm{3}{ab}\right)^{\mathrm{2}} }{\mathrm{3}\left({a}+{b}\right)^{\mathrm{2}} }−\frac{\mathrm{3}{a}^{\mathrm{2}} {b}}{{a}+{b}}+{a}^{\mathrm{2}} }= \\ $$$$=\sqrt{\frac{{a}^{\mathrm{2}} }{\left({a}+{b}\right)^{\mathrm{2}} }\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right)}=\frac{{a}}{{a}+{b}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$$\mathrm{similar} \\ $$$$\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{3}}−{bx}+{b}^{\mathrm{2}} }=\frac{{b}}{{a}+{b}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$$\mathrm{and} \\ $$$$\frac{{a}}{{a}+{b}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} }+\frac{{b}}{{a}+{b}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} }= \\ $$$$=\frac{{a}+{b}}{{a}+{b}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} }=\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$
Commented by mathsuji last updated on 15/May/21
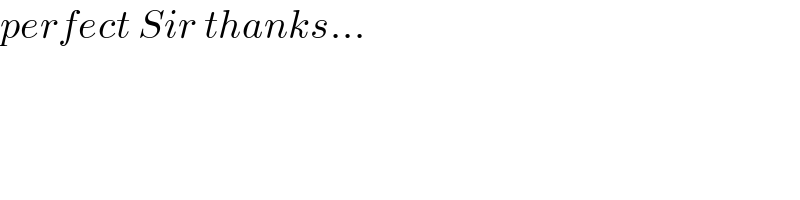
$${perfect}\:{Sir}\:{thanks}… \\ $$
