Question Number 141085 by iloveisrael last updated on 15/May/21
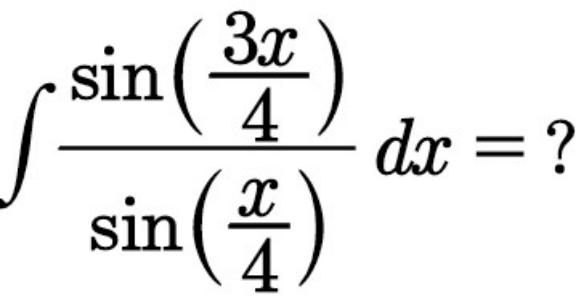
Answered by mindispower last updated on 15/May/21
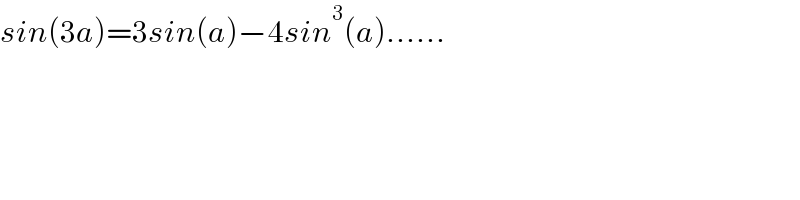
$${sin}\left(\mathrm{3}{a}\right)=\mathrm{3}{sin}\left({a}\right)−\mathrm{4}{sin}^{\mathrm{3}} \left({a}\right)…… \\ $$
Answered by qaz last updated on 15/May/21
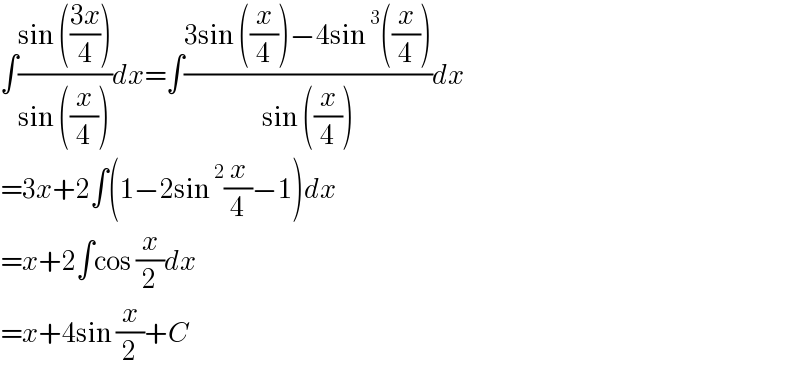
$$\int\frac{\mathrm{sin}\:\left(\frac{\mathrm{3}{x}}{\mathrm{4}}\right)}{\mathrm{sin}\:\left(\frac{{x}}{\mathrm{4}}\right)}{dx}=\int\frac{\mathrm{3sin}\:\left(\frac{{x}}{\mathrm{4}}\right)−\mathrm{4sin}\:^{\mathrm{3}} \left(\frac{{x}}{\mathrm{4}}\right)}{\mathrm{sin}\:\left(\frac{{x}}{\mathrm{4}}\right)}{dx} \\ $$$$=\mathrm{3}{x}+\mathrm{2}\int\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \frac{{x}}{\mathrm{4}}−\mathrm{1}\right){dx} \\ $$$$={x}+\mathrm{2}\int\mathrm{cos}\:\frac{{x}}{\mathrm{2}}{dx} \\ $$$$={x}+\mathrm{4sin}\:\frac{{x}}{\mathrm{2}}+{C} \\ $$
