Menu Close

Question-141124

Tinku Tara 0 Comments
Pin




Question Number 141124 by iloveisrael last updated on 16/May/21
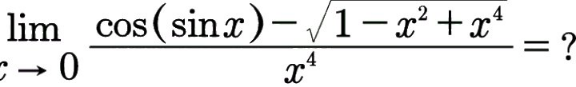
Answered by bobhans last updated on 16/May/21
Answered by EDWIN88 last updated on 16/May/21
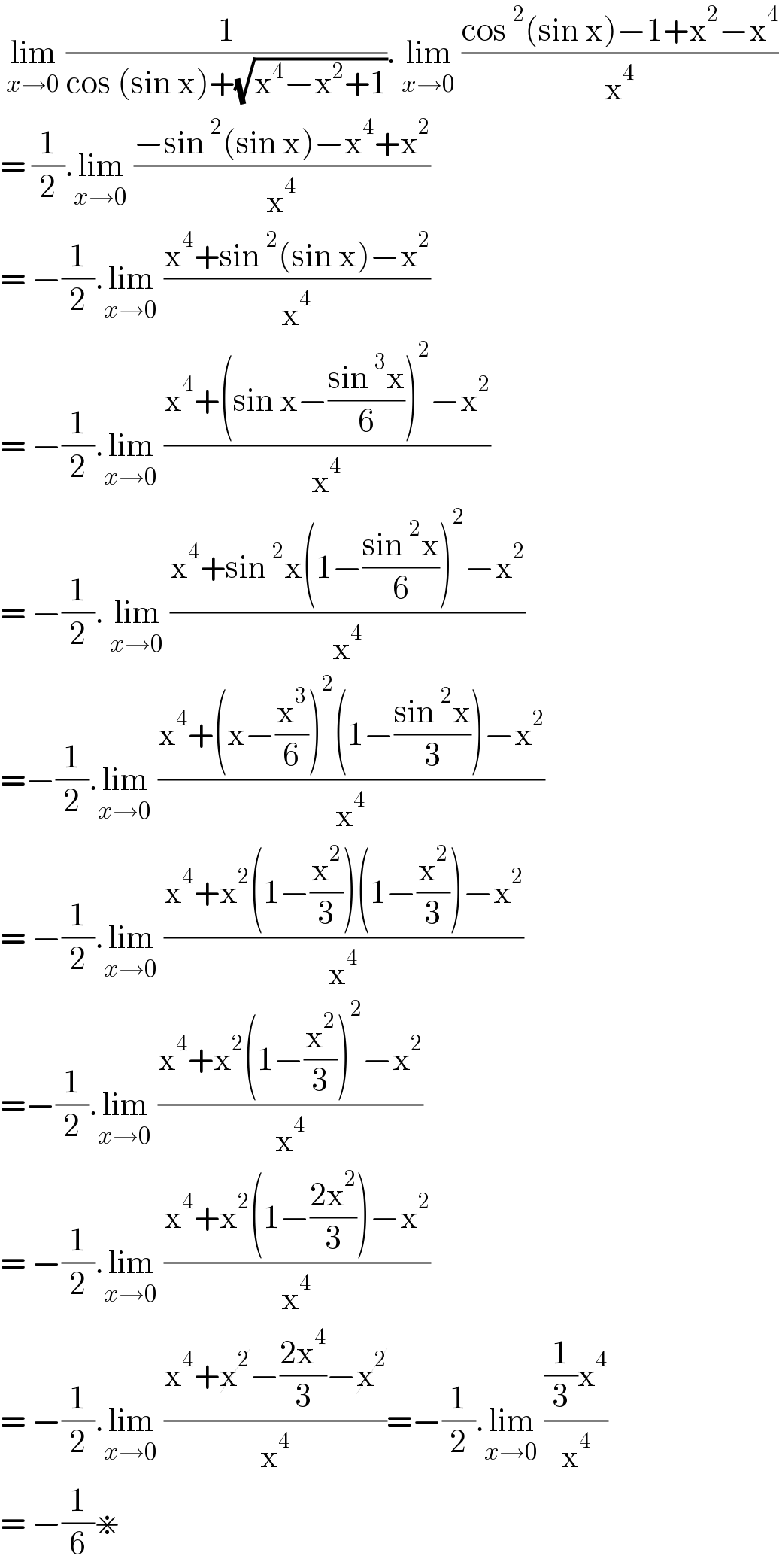
lim_(x→0) (1/(cos (sin x)+(√(x^4 −x^2 +1)))). lim_(x→0) ((cos^2 (sin x)−1+x^2 −x^4 )/x^4 ) = (1/2).lim_(x→0) ((−sin^2 (sin x)−x^4 +x^2 )/x^4 ) = −(1/2).lim_(x→0) ((x^4 +sin^2 (sin x)−x^2 )/x^4 ) = −(1/2).lim_(x→0) ((x^4 +(sin x−((sin^3 x)/6))^2 −x^2 )/x^4 ) = −(1/2). lim_(x→0) ((x^4 +sin^2 x(1−((sin^2 x)/6))^2 −x^2 )/x^4 ) =−(1/2).lim_(x→0) ((x^4 +(x−(x^3 /6))^2 (1−((sin^2 x)/3))−x^2 )/x^4 ) = −(1/2).lim_(x→0) ((x^4 +x^2 (1−(x^2 /3))(1−(x^2 /3))−x^2 )/x^4 ) =−(1/2).lim_(x→0) ((x^4 +x^2 (1−(x^2 /3))^2 −x^2 )/x^4 ) = −(1/2).lim_(x→0) ((x^4 +x^2 (1−((2x^2 )/3))−x^2 )/x^4 ) = −(1/2).lim_(x→0) ((x^4 +x^2 −((2x^4 )/3)−x^2 )/x^4 )=−(1/2).lim_(x→0) (((1/3)x^4 )/x^4 ) = −(1/6)⋇
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:\left(\mathrm{sin}\:\mathrm{x}\right)+\sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{sin}\:\mathrm{x}\right)−\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:\mathrm{x}\right)−\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{sin}\:\mathrm{x}\right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\left(\mathrm{sin}\:\mathrm{x}−\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{3}}\right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{3}}\right)−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{x}^{\mathrm{4}} +\cancel{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{2x}^{\mathrm{4}} }{\mathrm{3}}−\cancel{\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}^{\mathrm{4}} }=−\frac{\mathrm{1}}{\mathrm{2}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{4}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{6}}\divideontimes\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *