Question Number 141153 by iloveisrael last updated on 16/May/21

Answered by iloveisrael last updated on 16/May/21

Commented by SamuelAsaana last updated on 16/May/21
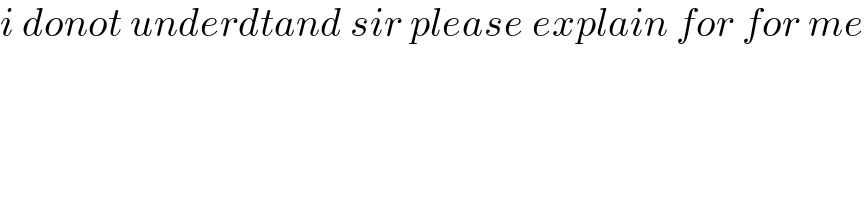
$${i}\:{donot}\:{underdtand}\:{sir}\:{please}\:{explain}\:{for}\:{for}\:{me} \\ $$
Answered by mr W last updated on 16/May/21
![(x−y)^3 =5((√3)−(√2)) ⇒x−y=((5((√3)−(√2))))^(1/3) (x+y)^3 −6xy(x+y)=5((√3)+(√2)) (x+y)^3 −(3/2)((x+y)^2 −(x−y)^2 )(x+y)=5((√3)+(√2)) (x+y)^3 −3((25(5−2(√6))))^(1/3) (x+y)+10((√3)+(√2))=0 Δ=−25(5−2(√6))+25(5+2(√6))=100(√6)>0 ⇒x+y=((10(6)^(1/4) −5((√3)+(√2))))^(1/3) −((10(6)^(1/4) +5((√3)+(√2)))^(1/3) ) x=(1/2)[((10(6)^(1/4) −5((√3)+(√2))))^(1/3) −((10(6)^(1/4) +5((√3)+(√2))))^(1/3) +((5((√3)−(√2))))^(1/3) ]≈−1.209505 y=(1/2)[((10(6)^(1/4) −5((√3)+(√2))))^(1/3) −((10(6)^(1/4) +5((√3)+(√2))))^(1/3) −((5((√3)−(√2))))^(1/3) ]≈−2.376472](https://www.tinkutara.com/question/Q141161.png)
$$\left({x}−{y}\right)^{\mathrm{3}} =\mathrm{5}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}−{y}=\sqrt[{\mathrm{3}}]{\mathrm{5}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)} \\ $$$$ \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{6}{xy}\left({x}+{y}\right)=\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right) \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}\left(\left({x}+{y}\right)^{\mathrm{2}} −\left({x}−{y}\right)^{\mathrm{2}} \right)\left({x}+{y}\right)=\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right) \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{25}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)}\left({x}+{y}\right)+\mathrm{10}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Delta=−\mathrm{25}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)+\mathrm{25}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)=\mathrm{100}\sqrt{\mathrm{6}}>\mathrm{0} \\ $$$$\left.\Rightarrow{x}+{y}=\sqrt[{\mathrm{3}}]{\mathrm{10}\sqrt[{\mathrm{4}}]{\mathrm{6}}−\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)}−\sqrt[{\mathrm{3}}]{\mathrm{10}\sqrt[{\mathrm{4}}]{\mathrm{6}}+\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right.}\right) \\ $$$$ \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt[{\mathrm{3}}]{\mathrm{10}\sqrt[{\mathrm{4}}]{\mathrm{6}}−\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)}−\sqrt[{\mathrm{3}}]{\mathrm{10}\sqrt[{\mathrm{4}}]{\mathrm{6}}+\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)}+\sqrt[{\mathrm{3}}]{\mathrm{5}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)}\right]\approx−\mathrm{1}.\mathrm{209505} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt[{\mathrm{3}}]{\mathrm{10}\sqrt[{\mathrm{4}}]{\mathrm{6}}−\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)}−\sqrt[{\mathrm{3}}]{\mathrm{10}\sqrt[{\mathrm{4}}]{\mathrm{6}}+\mathrm{5}\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}\right)}−\sqrt[{\mathrm{3}}]{\mathrm{5}\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)}\right]\approx−\mathrm{2}.\mathrm{376472} \\ $$
Commented by iloveisrael last updated on 16/May/21

$$\mathrm{Y}{es} \\ $$
