Question-141163

Question Number 141163 by Niiicooooo last updated on 16/May/21

Answered by mindispower last updated on 16/May/21

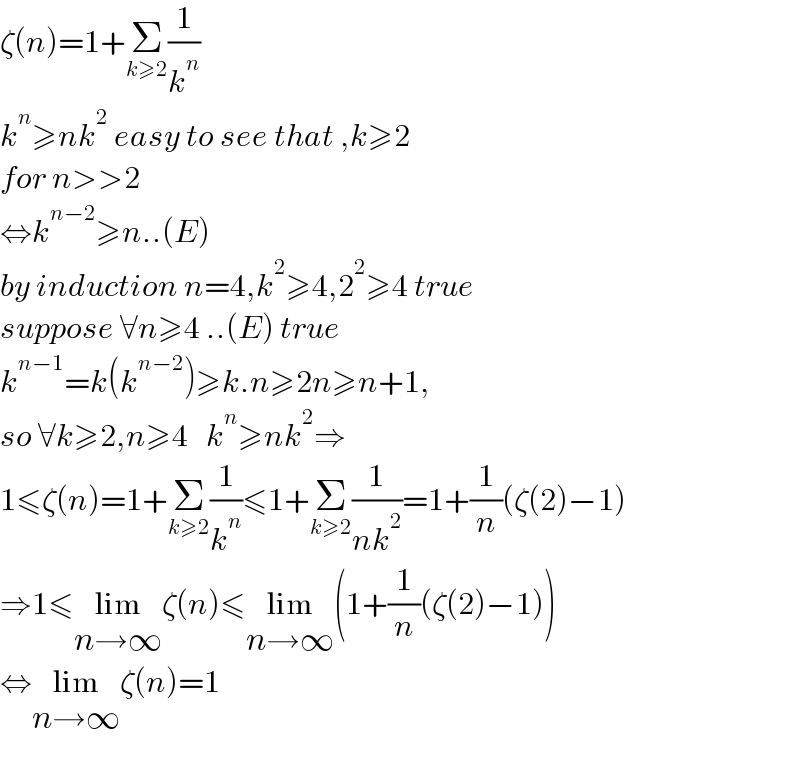
ζ(n)=1+Σ_(k≥2) (1/k^n ) k^n ≥nk^2 easy to see that ,k≥2 for n>>2 ⇔k^(n−2) ≥n..(E) by induction n=4,k^2 ≥4,2^2 ≥4 true suppose ∀n≥4 ..(E) true k^(n−1) =k(k^(n−2) )≥k.n≥2n≥n+1, so ∀k≥2,n≥4 k^n ≥nk^2 ⇒ 1≤ζ(n)=1+Σ_(k≥2) (1/k^n )≤1+Σ_(k≥2) (1/(nk^2 ))=1+(1/n)(ζ(2)−1) ⇒1≤lim_(n→∞) ζ(n)≤lim_(n→∞) (1+(1/n)(ζ(2)−1)) ⇔lim_(n→∞) ζ(n)=1

$$\zeta\left({n}\right)=\mathrm{1}+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{{k}^{{n}} } \\ $$$${k}^{{n}} \geqslant{nk}^{\mathrm{2}} \:{easy}\:{to}\:{see}\:{that}\:,{k}\geqslant\mathrm{2} \\ $$$${for}\:{n}>>\mathrm{2} \\ $$$$\Leftrightarrow{k}^{{n}−\mathrm{2}} \geqslant{n}..\left({E}\right) \\ $$$${by}\:{induction}\:{n}=\mathrm{4},{k}^{\mathrm{2}} \geqslant\mathrm{4},\mathrm{2}^{\mathrm{2}} \geqslant\mathrm{4}\:{true} \\ $$$${suppose}\:\forall{n}\geqslant\mathrm{4}\:..\left({E}\right)\:{true}\: \\ $$$${k}^{{n}−\mathrm{1}} ={k}\left({k}^{{n}−\mathrm{2}} \right)\geqslant{k}.{n}\geqslant\mathrm{2}{n}\geqslant{n}+\mathrm{1}, \\ $$$${so}\:\forall{k}\geqslant\mathrm{2},{n}\geqslant\mathrm{4}\:\:\:{k}^{{n}} \geqslant{nk}^{\mathrm{2}} \Rightarrow \\ $$$$\mathrm{1}\leqslant\zeta\left({n}\right)=\mathrm{1}+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{{k}^{{n}} }\leqslant\mathrm{1}+\underset{{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{1}}{{nk}^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{1}}{{n}}\left(\zeta\left(\mathrm{2}\right)−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{1}\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\zeta\left({n}\right)\leqslant\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\left(\zeta\left(\mathrm{2}\right)−\mathrm{1}\right)\right) \\ $$$$\Leftrightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\zeta\left({n}\right)=\mathrm{1} \\ $$$$ \\ $$

Commented by Niiicooooo last updated on 17/May/21

$${greatful} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply