Menu Close

Question-141171

Tinku Tara 0 Comments
Pin




Question Number 141171 by iloveisrael last updated on 16/May/21
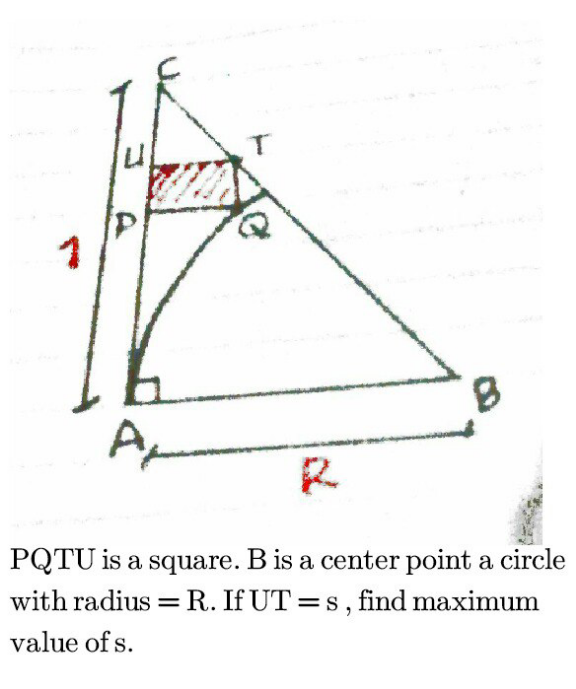
Commented by iloveisrael last updated on 16/May/21
insteresting question
$$\:{insteresting}\:{question} \\ $$
Commented by mr W last updated on 16/May/21
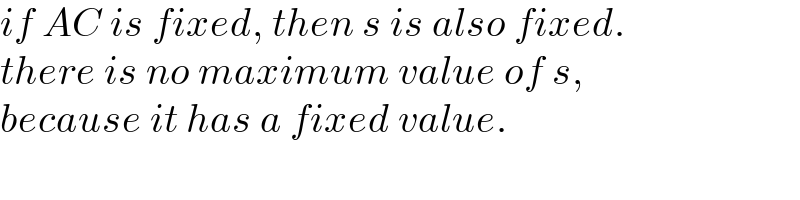
if AC is fixed, then s is also fixed. there is no maximum value of s, because it has a fixed value.
$${if}\:{AC}\:{is}\:{fixed},\:{then}\:{s}\:{is}\:{also}\:{fixed}. \\ $$$${there}\:{is}\:{no}\:{maximum}\:{value}\:{of}\:{s}, \\ $$$${because}\:{it}\:{has}\:{a}\:{fixed}\:{value}. \\ $$
Commented by iloveisrael last updated on 16/May/21
no
$${no} \\ $$
Commented by mr W last updated on 16/May/21
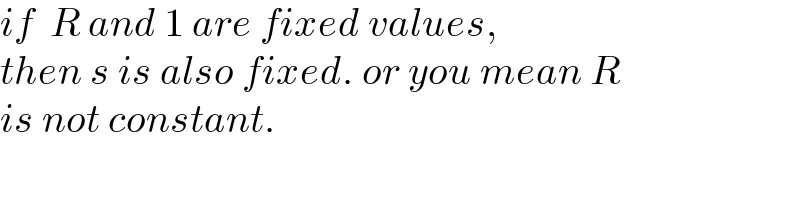
if R and 1 are fixed values, then s is also fixed. or you mean R is not constant.
$${if}\:\:{R}\:{and}\:\mathrm{1}\:{are}\:{fixed}\:{values}, \\ $$$${then}\:{s}\:{is}\:{also}\:{fixed}.\:{or}\:{you}\:{mean}\:{R} \\ $$$${is}\:{not}\:{constant}. \\ $$
Commented by EDWIN88 last updated on 16/May/21
s depent to r . not a constant
$$\mathrm{s}\:\mathrm{depent}\:\mathrm{to}\:\mathrm{r}\:.\:\mathrm{not}\:\mathrm{a}\:\mathrm{constant} \\ $$
Commented by mr W last updated on 16/May/21
but if r is constant, then s is also constant. the question seems to show that r is given, i.e. r is constant.
$${but}\:{if}\:{r}\:{is}\:{constant},\:{then}\:{s}\:{is}\:{also} \\ $$$${constant}.\:{the}\:{question}\:{seems}\:{to}\:{show} \\ $$$${that}\:{r}\:{is}\:{given},\:{i}.{e}.\:{r}\:{is}\:{constant}. \\ $$
Answered by EDWIN88 last updated on 16/May/21
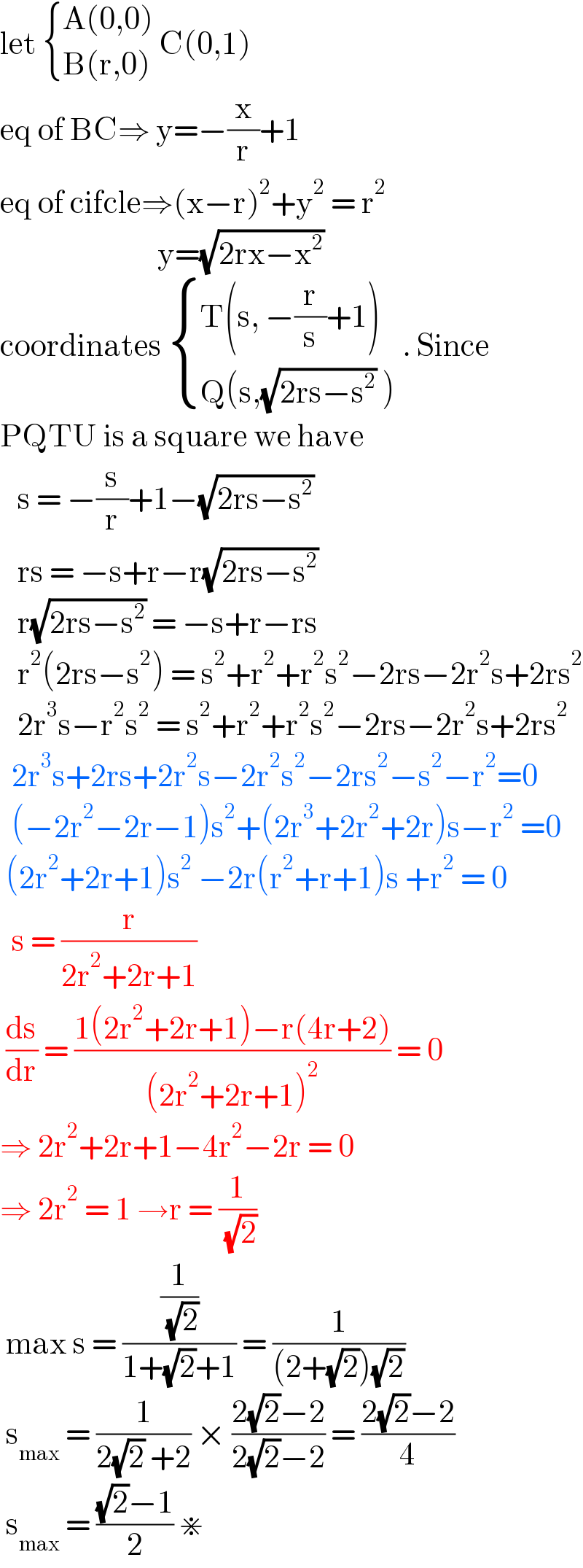
let { ((A(0,0) )),((B(r,0))) :}C(0,1) eq of BC⇒ y=−(x/r)+1 eq of cifcle⇒(x−r)^2 +y^2 = r^2 y=(√(2rx−x^2 )) coordinates { ((T(s, −(r/s)+1))),((Q(s,(√(2rs−s^2 )) ))) :} . Since PQTU is a square we have s = −(s/r)+1−(√(2rs−s^2 )) rs = −s+r−r(√(2rs−s^2 )) r(√(2rs−s^2 )) = −s+r−rs r^2 (2rs−s^2 ) = s^2 +r^2 +r^2 s^2 −2rs−2r^2 s+2rs^2 2r^3 s−r^2 s^2 = s^2 +r^2 +r^2 s^2 −2rs−2r^2 s+2rs^2 2r^3 s+2rs+2r^2 s−2r^2 s^2 −2rs^2 −s^2 −r^2 =0 (−2r^2 −2r−1)s^2 +(2r^3 +2r^2 +2r)s−r^2 =0 (2r^2 +2r+1)s^2 −2r(r^2 +r+1)s +r^2 = 0 s = (r/(2r^2 +2r+1)) (ds/dr) = ((1(2r^2 +2r+1)−r(4r+2))/((2r^2 +2r+1)^2 )) = 0 ⇒ 2r^2 +2r+1−4r^2 −2r = 0 ⇒ 2r^2 = 1 →r = (1/( (√2))) max s = ((1/( (√2)))/(1+(√2)+1)) = (1/((2+(√2))(√2))) s_(max) = (1/(2(√2) +2)) × ((2(√2)−2)/(2(√2)−2)) = ((2(√2)−2)/4) s_(max) = (((√2)−1)/2) ⋇
$$\mathrm{let}\:\begin{cases}{\mathrm{A}\left(\mathrm{0},\mathrm{0}\right)\:}\\{\mathrm{B}\left(\mathrm{r},\mathrm{0}\right)}\end{cases}\mathrm{C}\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\mathrm{eq}\:\mathrm{of}\:\mathrm{BC}\Rightarrow\:\mathrm{y}=−\frac{\mathrm{x}}{\mathrm{r}}+\mathrm{1} \\ $$$$\mathrm{eq}\:\mathrm{of}\:\mathrm{cifcle}\Rightarrow\left(\mathrm{x}−\mathrm{r}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{r}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}=\sqrt{\mathrm{2rx}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{coordinates}\:\begin{cases}{\mathrm{T}\left(\mathrm{s},\:−\frac{\mathrm{r}}{\mathrm{s}}+\mathrm{1}\right)}\\{\mathrm{Q}\left(\mathrm{s},\sqrt{\mathrm{2rs}−\mathrm{s}^{\mathrm{2}} }\:\right)}\end{cases}\:.\:\mathrm{Since} \\ $$$$\mathrm{PQTU}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square}\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\:\:\:\mathrm{s}\:=\:−\frac{\mathrm{s}}{\mathrm{r}}+\mathrm{1}−\sqrt{\mathrm{2rs}−\mathrm{s}^{\mathrm{2}} } \\ $$$$\:\:\:\mathrm{rs}\:=\:−\mathrm{s}+\mathrm{r}−\mathrm{r}\sqrt{\mathrm{2rs}−\mathrm{s}^{\mathrm{2}} } \\ $$$$\:\:\:\mathrm{r}\sqrt{\mathrm{2rs}−\mathrm{s}^{\mathrm{2}} }\:=\:−\mathrm{s}+\mathrm{r}−\mathrm{rs} \\ $$$$\:\:\:\mathrm{r}^{\mathrm{2}} \left(\mathrm{2rs}−\mathrm{s}^{\mathrm{2}} \right)\:=\:\mathrm{s}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} −\mathrm{2rs}−\mathrm{2r}^{\mathrm{2}} \mathrm{s}+\mathrm{2rs}^{\mathrm{2}} \\ $$$$\:\:\:\mathrm{2r}^{\mathrm{3}} \mathrm{s}−\mathrm{r}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} \:=\:\mathrm{s}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} −\mathrm{2rs}−\mathrm{2r}^{\mathrm{2}} \mathrm{s}+\mathrm{2rs}^{\mathrm{2}} \\ $$$$\:\:\mathrm{2r}^{\mathrm{3}} \mathrm{s}+\mathrm{2rs}+\mathrm{2r}^{\mathrm{2}} \mathrm{s}−\mathrm{2r}^{\mathrm{2}} \mathrm{s}^{\mathrm{2}} −\mathrm{2rs}^{\mathrm{2}} −\mathrm{s}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\left(−\mathrm{2r}^{\mathrm{2}} −\mathrm{2r}−\mathrm{1}\right)\mathrm{s}^{\mathrm{2}} +\left(\mathrm{2r}^{\mathrm{3}} +\mathrm{2r}^{\mathrm{2}} +\mathrm{2r}\right)\mathrm{s}−\mathrm{r}^{\mathrm{2}} \:=\mathrm{0} \\ $$$$\:\left(\mathrm{2r}^{\mathrm{2}} +\mathrm{2r}+\mathrm{1}\right)\mathrm{s}^{\mathrm{2}} \:−\mathrm{2r}\left(\mathrm{r}^{\mathrm{2}} +\mathrm{r}+\mathrm{1}\right)\mathrm{s}\:+\mathrm{r}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\:\:\mathrm{s}\:=\:\frac{\mathrm{r}}{\mathrm{2r}^{\mathrm{2}} +\mathrm{2r}+\mathrm{1}} \\ $$$$\:\frac{\mathrm{ds}}{\mathrm{dr}}\:=\:\frac{\mathrm{1}\left(\mathrm{2r}^{\mathrm{2}} +\mathrm{2r}+\mathrm{1}\right)−\mathrm{r}\left(\mathrm{4r}+\mathrm{2}\right)}{\left(\mathrm{2r}^{\mathrm{2}} +\mathrm{2r}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2r}^{\mathrm{2}} +\mathrm{2r}+\mathrm{1}−\mathrm{4r}^{\mathrm{2}} −\mathrm{2r}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2r}^{\mathrm{2}} \:=\:\mathrm{1}\:\rightarrow\mathrm{r}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:\mathrm{max}\:\mathrm{s}\:=\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}+\sqrt{\mathrm{2}}+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)\sqrt{\mathrm{2}}} \\ $$$$\:\mathrm{s}_{\mathrm{max}} \:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2}}\:×\:\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}{\mathrm{4}} \\ $$$$\:\mathrm{s}_{\mathrm{max}} \:=\:\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\mathrm{2}}\:\divideontimes\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *