Question Number 141186 by SLVR last updated on 16/May/21

Commented by SLVR last updated on 16/May/21

$${Good}\:{evening}\:{sir}..\:{Mr}.{Dwaipayan}.. \\ $$$${i}\:{forgotten}\:{to}\:{write}\:{your}\:{explanation} \\ $$
Commented by SLVR last updated on 16/May/21

$${kindly}\:{resend}\:{me}\:{your}\:{solution} \\ $$$${taken}\:{with}\:{integration}\:{by}\:{parts} \\ $$$${please}… \\ $$
Commented by Ar Brandon last updated on 16/May/21

$$\mathrm{You}\:\mathrm{may}\:\mathrm{tap}\:\mathrm{your}\:\mathrm{username}\:\mathrm{to}\:\mathrm{sort} \\ $$$$\mathrm{your}\:\mathrm{posts} \\ $$
Commented by Ar Brandon last updated on 16/May/21

$$\mathrm{Q139811} \\ $$
Answered by Ar Brandon last updated on 16/May/21
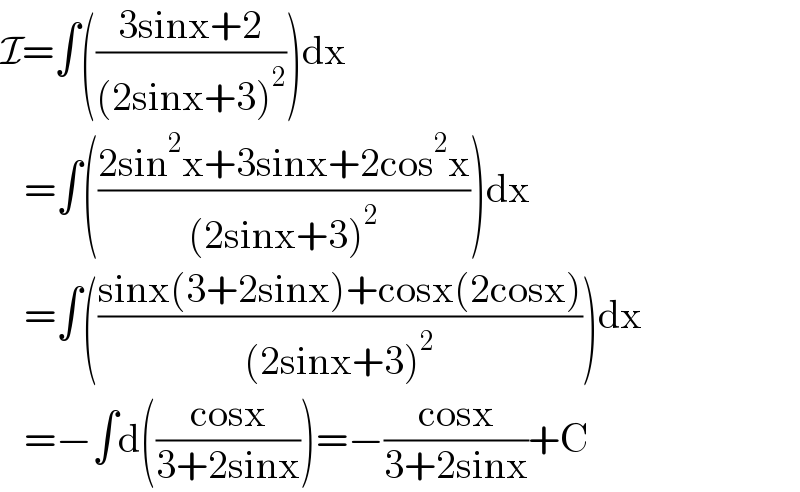
$$\mathcal{I}=\int\left(\frac{\mathrm{3sinx}+\mathrm{2}}{\left(\mathrm{2sinx}+\mathrm{3}\right)^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$\:\:\:=\int\left(\frac{\mathrm{2sin}^{\mathrm{2}} \mathrm{x}+\mathrm{3sinx}+\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{2sinx}+\mathrm{3}\right)^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$\:\:\:=\int\left(\frac{\mathrm{sinx}\left(\mathrm{3}+\mathrm{2sinx}\right)+\mathrm{cosx}\left(\mathrm{2cosx}\right)}{\left(\mathrm{2sinx}+\mathrm{3}\right)^{\mathrm{2}} }\right)\mathrm{dx} \\ $$$$\:\:\:=−\int\mathrm{d}\left(\frac{\mathrm{cosx}}{\mathrm{3}+\mathrm{2sinx}}\right)=−\frac{\mathrm{cosx}}{\mathrm{3}+\mathrm{2sinx}}+\mathrm{C} \\ $$
Commented by Ar Brandon last updated on 16/May/21

😉😃
Commented by SLVR last updated on 16/May/21
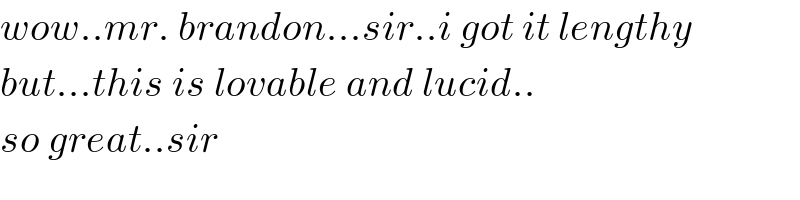
$${wow}..{mr}.\:{brandon}…{sir}..{i}\:{got}\:{it}\:{lengthy} \\ $$$${but}…{this}\:{is}\:{lovable}\:{and}\:{lucid}.. \\ $$$${so}\:{great}..{sir} \\ $$
