Question Number 141227 by ajfour last updated on 16/May/21
Commented by ajfour last updated on 16/May/21
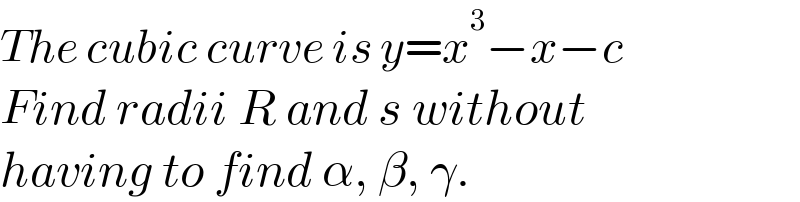
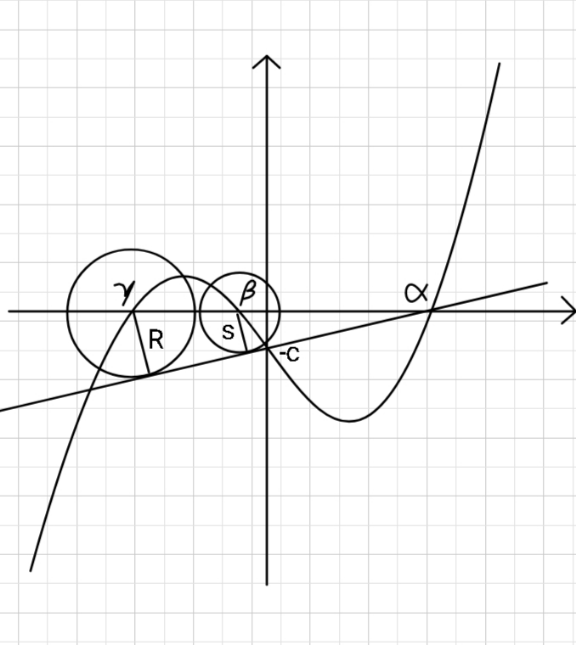
$${The}\:{cubic}\:{curve}\:{is}\:{y}={x}^{\mathrm{3}} −{x}−{c} \\ $$$${Find}\:{radii}\:{R}\:{and}\:{s}\:{without} \\ $$$${having}\:{to}\:{find}\:\alpha,\:\beta,\:\gamma. \\ $$
Commented by MJS_new last updated on 17/May/21

$$\mathrm{just}\:\mathrm{a}\:\mathrm{thought}:\:\mathrm{if}\:\mathrm{we}\:\mathrm{let} \\ $$$${c}={a}\left({a}^{\mathrm{2}} −\mathrm{1}\right)\wedge{a}>\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{gets} \\ $$$${x}^{\mathrm{3}} −{x}−{a}\left({a}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{solutions} \\ $$$$\alpha={a} \\ $$$$\beta=−\frac{{a}}{\mathrm{2}}+\frac{\sqrt{\mathrm{4}−\mathrm{3}{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\gamma=−\frac{{a}}{\mathrm{2}}−\frac{\sqrt{\mathrm{4}−\mathrm{3}{a}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{connecting} \\ $$$$\begin{pmatrix}{\alpha}\\{\mathrm{0}}\end{pmatrix}\:\mathrm{and}\:\begin{pmatrix}{\mathrm{0}}\\{−{c}}\end{pmatrix}\:\mathrm{is} \\ $$$$\left({a}^{\mathrm{2}} −\mathrm{1}\right){x}+{y}−{a}\left({a}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${R}=\frac{\mid\left({a}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{3}{a}+\sqrt{\mathrm{4}−\mathrm{3}{a}^{\mathrm{2}} }\right)\mid}{\:\mathrm{2}\sqrt{{a}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}}} \\ $$$${r}=\frac{\mid\left({a}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{3}{a}−\sqrt{\mathrm{4}−\mathrm{3}{a}^{\mathrm{2}} }\right)\mid}{\:\mathrm{2}\sqrt{{a}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}}} \\ $$$$\mathrm{of}\:\mathrm{course}\:\mathrm{the}\:\mathrm{original}\:\mathrm{problem}\:\mathrm{is}\:\mathrm{not}\:\mathrm{solved} \\ $$$$\mathrm{because}\:{c}={a}\left({a}^{\mathrm{2}} −\mathrm{1}\right)\:\Leftrightarrow\:{a}^{\mathrm{3}} −{a}−{c}=\mathrm{0}\:\mathrm{so}\:\mathrm{finding} \\ $$$${a}\:\mathrm{for}\:\mathrm{a}\:\mathrm{given}\:{c}\:\mathrm{leads}\:\mathrm{back}\:\mathrm{to}\:\mathrm{the}\:\mathrm{start}\:\infty \\ $$
Answered by ajfour last updated on 17/May/21
Commented by ajfour last updated on 17/May/21
![α=(√(p^2 −c^2 )) β=α−q γ=α−r α+β+γ=0 αβ+βγ+γα=−1 αβ γ= c (q/r)=(s/R) (c/p)=(s/q)=(R/r) ⇒ c+s+R=0 let (q/r)=(s/R)=k ⇒ q=kr 2α=q+r−(√(p^2 −c^2 )) 2β= r−(√(p^2 −c^2 )) 2γ= q−(√(p^2 −c^2 )) ⇒ q+r=(3/2)(√(p^2 −c^2 )) ...(i) (q+r)^2 +2(p^2 −c^2 ) −3(√(p^2 −c^2 )) (q+r) +qr+(p^2 −c^2 ) −(√(p^2 −c^2 ))(q+r)=−4 ⇒ (q+r)^2 +3(p^2 −c^2 ) −4(√(p^2 −c^2 ))(q+r)+4+qr=0 .....(ii) (q+r−(√(p^2 −c^2 ))) ×{qr+(p^2 −c^2 )−(√(p^2 −c^2 ))(q+r)} =8c ....(iii) simplifying (ii) −(3/4)(p^2 −c^2 )+4+qr = 0 ..(I) now taking up (iii) −(5/2)(√(p^2 −c^2 ))(qr−((√(p^2 −c^2 ))/2)) =8c using (I) in here→ −(5/2)((2/( (√3))))(√(4+qr))(qr−((√(4+qr))/( (√3)))) = 8c let qr=4tan^2 θ ⇒ sec θ(tan^2 θ−(1/( 2(√3)))sec θ) +(((√3)c)/5) = 0 AB=−(((√3)c)/5) B=A^2 −1−(A/(2(√3))) ⇒ (((√3)c)/(5A))+(A/(2(√3)))=A(A−(1/A)) ⇒ A=(((A/(2(√3)))+(((√3)c)/(5A)))/(A−(1/A))) = (((A^2 /(2(√3)))+(((√3)c)/5))/(A^2 −1)) A^2 =(((A^4 /(12))+(A^2 /(10))+((3c^2 )/(25)))/(A^4 −2A^2 +1)) ⇒ 60A^2 (A^2 −1)^2 =5(A^2 +(3/5))^2 −(9/5)+((36c^2 )/5) let A^2 = t+b ⇒ 60(t+b)(t+b−1)^2 = 5(t+b+(3/5))^2 −(9/5)+((36c^2 )/5) 60{t^3 +b(4b−3)t^2 + [(b−1)^2 +2b(b−2)]t+b(b−1)^2 } = 5t^2 +10(b+(3/5))t +5(b+(3/5))^2 −(9/5)+((36c^2 )/5) ⇒ 60t^3 +5(48b^2 −36b−1)t^2 +2(90b^2 −185b+27)t +(60b^3 −125b^2 +54b+((36c^2 )/5)) = 0 .....(★) let 5(48b^2 −36b−1)^2 =72(90b^2 −185b+27) Nice eq. I saw the exact answer and ran away asap..! otherwise let→ 48b^2 −36b−1=0 ⇒ 3(4b)^2 −9(4b)−1=0 4b=(3/2)±(√((9/4)+(1/3))) b=((6±(√(62)))/(16)) Now P =90b^2 −185b+27 = 540b+15−185b+27 =355b+42 The positive b=((6+(√(62)))/(16)) should lead to the answer.. (3/4)α^2 =4+qr ∀ qr>−4 qr= 4(A^2 −1) =4(t+b−1) ⇒ t >−b and i checked that for chosen b, t>0>−b b is known, we get t from(★)](https://www.tinkutara.com/question/Q141254.png)
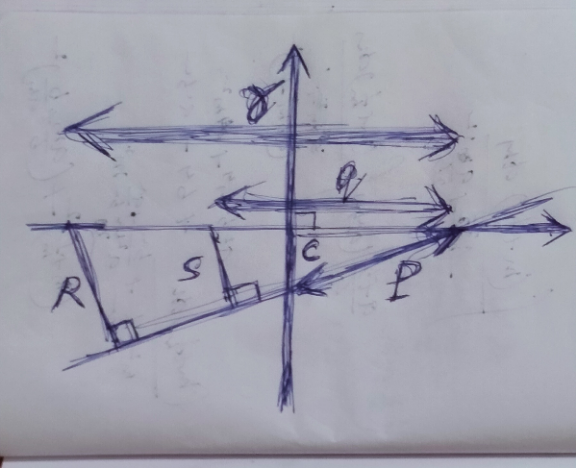
$$\alpha=\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\beta=\alpha−{q} \\ $$$$\gamma=\alpha−{r} \\ $$$$\alpha+\beta+\gamma=\mathrm{0} \\ $$$$\alpha\beta+\beta\gamma+\gamma\alpha=−\mathrm{1} \\ $$$$\alpha\beta\:\gamma=\:{c} \\ $$$$\frac{{q}}{{r}}=\frac{{s}}{{R}} \\ $$$$\frac{{c}}{{p}}=\frac{{s}}{{q}}=\frac{{R}}{{r}} \\ $$$$\Rightarrow\:\:{c}+{s}+{R}=\mathrm{0} \\ $$$${let}\:\:\frac{{q}}{{r}}=\frac{{s}}{{R}}={k} \\ $$$$\Rightarrow\:\:{q}={kr} \\ $$$$\mathrm{2}\alpha={q}+{r}−\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\mathrm{2}\beta=\:{r}−\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\mathrm{2}\gamma=\:{q}−\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{q}+{r}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\:\:\:\:…\left({i}\right) \\ $$$$\left({q}+{r}\right)^{\mathrm{2}} +\mathrm{2}\left({p}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$$$\:\:\:−\mathrm{3}\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\:\left({q}+{r}\right) \\ $$$$\:\:+{qr}+\left({p}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$$$\:−\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\left({q}+{r}\right)=−\mathrm{4} \\ $$$$\Rightarrow \\ $$$$\left({q}+{r}\right)^{\mathrm{2}} +\mathrm{3}\left({p}^{\mathrm{2}} −{c}^{\mathrm{2}} \right) \\ $$$$\:−\mathrm{4}\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\left({q}+{r}\right)+\mathrm{4}+{qr}=\mathrm{0} \\ $$$$…..\left({ii}\right) \\ $$$$\left({q}+{r}−\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\right) \\ $$$$×\left\{{qr}+\left({p}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)−\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\left({q}+{r}\right)\right\} \\ $$$$=\mathrm{8}{c} \\ $$$$….\left({iii}\right) \\ $$$${simplifying}\:\left({ii}\right) \\ $$$$\:−\frac{\mathrm{3}}{\mathrm{4}}\left({p}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)+\mathrm{4}+{qr}\:=\:\mathrm{0}\:\:..\left({I}\right) \\ $$$${now}\:{taking}\:{up}\:\left({iii}\right) \\ $$$$−\frac{\mathrm{5}}{\mathrm{2}}\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }\left({qr}−\frac{\sqrt{{p}^{\mathrm{2}} −{c}^{\mathrm{2}} }}{\mathrm{2}}\right)\:=\mathrm{8}{c} \\ $$$$\:{using}\:\left({I}\right)\:{in}\:{here}\rightarrow \\ $$$$−\frac{\mathrm{5}}{\mathrm{2}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\right)\sqrt{\mathrm{4}+{qr}}\left({qr}−\frac{\sqrt{\mathrm{4}+{qr}}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\:\:=\:\mathrm{8}{c} \\ $$$${let}\:\:{qr}=\mathrm{4tan}\:^{\mathrm{2}} \theta\:\:\Rightarrow \\ $$$$\:\mathrm{sec}\:\theta\left(\mathrm{tan}\:^{\mathrm{2}} \theta−\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{sec}\:\theta\right) \\ $$$$\:\:\:+\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{5}}\:=\:\mathrm{0} \\ $$$$\:\:\:{AB}=−\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{5}} \\ $$$${B}={A}^{\mathrm{2}} −\mathrm{1}−\frac{{A}}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\:\:\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{5}{A}}+\frac{{A}}{\mathrm{2}\sqrt{\mathrm{3}}}={A}\left({A}−\frac{\mathrm{1}}{{A}}\right) \\ $$$$\Rightarrow\:\:{A}=\frac{\frac{{A}}{\mathrm{2}\sqrt{\mathrm{3}}}+\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{5}{A}}}{{A}−\frac{\mathrm{1}}{{A}}}\:=\:\frac{\frac{{A}^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{3}}}+\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{5}}}{{A}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:{A}^{\mathrm{2}} =\frac{\frac{{A}^{\mathrm{4}} }{\mathrm{12}}+\frac{{A}^{\mathrm{2}} }{\mathrm{10}}+\frac{\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{25}}}{{A}^{\mathrm{4}} −\mathrm{2}{A}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{60}{A}^{\mathrm{2}} \left({A}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\mathrm{5}\left({A}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{5}}+\frac{\mathrm{36}{c}^{\mathrm{2}} }{\mathrm{5}} \\ $$$${let}\:\:{A}^{\mathrm{2}} =\:{t}+{b}\:\:\Rightarrow \\ $$$$\mathrm{60}\left({t}+{b}\right)\left({t}+{b}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:=\:\mathrm{5}\left({t}+{b}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{5}}+\frac{\mathrm{36}{c}^{\mathrm{2}} }{\mathrm{5}} \\ $$$$\mathrm{60}\left\{{t}^{\mathrm{3}} +{b}\left(\mathrm{4}{b}−\mathrm{3}\right){t}^{\mathrm{2}} +\right. \\ $$$$\left.\:\left[\left({b}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}{b}\left({b}−\mathrm{2}\right)\right]{t}+{b}\left({b}−\mathrm{1}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:=\:\mathrm{5}{t}^{\mathrm{2}} +\mathrm{10}\left({b}+\frac{\mathrm{3}}{\mathrm{5}}\right){t} \\ $$$$\:\:\:\:\:\:+\mathrm{5}\left({b}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{5}}+\frac{\mathrm{36}{c}^{\mathrm{2}} }{\mathrm{5}} \\ $$$$\Rightarrow \\ $$$$\:\:\mathrm{60}{t}^{\mathrm{3}} +\mathrm{5}\left(\mathrm{48}{b}^{\mathrm{2}} −\mathrm{36}{b}−\mathrm{1}\right){t}^{\mathrm{2}} \\ $$$$\:\:+\mathrm{2}\left(\mathrm{90}{b}^{\mathrm{2}} −\mathrm{185}{b}+\mathrm{27}\right){t} \\ $$$$\:\:+\left(\mathrm{60}{b}^{\mathrm{3}} −\mathrm{125}{b}^{\mathrm{2}} +\mathrm{54}{b}+\frac{\mathrm{36}{c}^{\mathrm{2}} }{\mathrm{5}}\right) \\ $$$$\:=\:\mathrm{0}\:\:\:\:\:\:…..\left(\bigstar\right) \\ $$$${let}\:\:\mathrm{5}\left(\mathrm{48}{b}^{\mathrm{2}} −\mathrm{36}{b}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{72}\left(\mathrm{90}{b}^{\mathrm{2}} −\mathrm{185}{b}+\mathrm{27}\right) \\ $$$$\mathcal{N}{ice}\:{eq}.\:{I}\:{saw}\:{the}\:{exact}\:{answer} \\ $$$$\:{and}\:{ran}\:{away}\:{asap}..! \\ $$$${otherwise}\:{let}\rightarrow \\ $$$$\:\:\mathrm{48}{b}^{\mathrm{2}} −\mathrm{36}{b}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{3}\left(\mathrm{4}{b}\right)^{\mathrm{2}} −\mathrm{9}\left(\mathrm{4}{b}\right)−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\mathrm{4}{b}=\frac{\mathrm{3}}{\mathrm{2}}\pm\sqrt{\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:{b}=\frac{\mathrm{6}\pm\sqrt{\mathrm{62}}}{\mathrm{16}} \\ $$$$\mathcal{N}{ow} \\ $$$$\:{P}\:=\mathrm{90}{b}^{\mathrm{2}} −\mathrm{185}{b}+\mathrm{27} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{540}{b}+\mathrm{15}−\mathrm{185}{b}+\mathrm{27} \\ $$$$\:\:=\mathrm{355}{b}+\mathrm{42} \\ $$$${The}\:{positive}\:{b}=\frac{\mathrm{6}+\sqrt{\mathrm{62}}}{\mathrm{16}} \\ $$$${should}\:{lead}\:{to}\:{the}\:{answer}.. \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\alpha^{\mathrm{2}} =\mathrm{4}+{qr}\:\:\:\:\:\forall\:\:{qr}>−\mathrm{4} \\ $$$${qr}=\:\mathrm{4}\left({A}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:=\mathrm{4}\left({t}+{b}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\:{t}\:>−{b}\:\:\:\: \\ $$$$\:\:{and}\:{i}\:{checked}\:{that}\:{for} \\ $$$${chosen}\:{b},\:{t}>\mathrm{0}>−{b} \\ $$$${b}\:{is}\:{known},\:{we}\:{get}\:{t}\:{from}\left(\bigstar\right) \\ $$
