Question-141308

Question Number 141308 by BHOOPENDRA last updated on 17/May/21

Answered by Dwaipayan Shikari last updated on 17/May/21

M=I+Σ_(n=1) ^∞ (t^n /(n!))A^n A= (((−3 −1)),((8 3)) )⇒A^2 = (((−3 −1)),(( 8 3)) ) (((−3 −1)),(( 8 3)) )= (((1 0)),((0 1)) )=I A^3 =IA M=I+Σ_(n=1) ^∞ (t^(2n) /((2n)!))A^(2n) +Σ_(n=0w) ^∞ (t^(2n+1) /((2n+1)!))A^(2n+1) A^(2n) =I =I+I(cosh (t)−1)+A(sinh (t)) =Icosh (t)+Asinh (t)

$$\boldsymbol{\mathrm{M}}=\boldsymbol{\mathrm{I}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{{n}} }{{n}!}\boldsymbol{\mathrm{A}}^{{n}} \\ $$$$\boldsymbol{\mathrm{A}}=\begin{pmatrix}{−\mathrm{3}\:−\mathrm{1}}\\{\mathrm{8}\:\:\:\:\:\mathrm{3}}\end{pmatrix}\Rightarrow\boldsymbol{\mathrm{A}}^{\mathrm{2}} =\begin{pmatrix}{−\mathrm{3}\:\:−\mathrm{1}}\\{\:\:\mathrm{8}\:\:\:\:\:\mathrm{3}}\end{pmatrix}\begin{pmatrix}{−\mathrm{3}\:\:−\mathrm{1}}\\{\:\:\:\mathrm{8}\:\:\:\:\mathrm{3}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\mathrm{0}}\\{\mathrm{0}\:\:\mathrm{1}}\end{pmatrix}=\boldsymbol{\mathrm{I}} \\ $$$$\boldsymbol{\mathrm{A}}^{\mathrm{3}} =\boldsymbol{\mathrm{IA}} \\ $$$$\boldsymbol{\mathrm{M}}=\boldsymbol{\mathrm{I}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{t}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}\boldsymbol{\mathrm{A}}^{\mathrm{2}{n}} +\underset{{n}=\mathrm{0}{w}} {\overset{\infty} {\sum}}\frac{{t}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\boldsymbol{\mathrm{A}}^{\mathrm{2}{n}+\mathrm{1}} \:\:\:\:\boldsymbol{\mathrm{A}}^{\mathrm{2}{n}} =\boldsymbol{\mathrm{I}} \\ $$$$=\boldsymbol{\mathrm{I}}+\boldsymbol{\mathrm{I}}\left(\mathrm{cosh}\:\left({t}\right)−\mathrm{1}\right)+\boldsymbol{\mathrm{A}}\left(\mathrm{sinh}\:\left({t}\right)\right) \\ $$$$=\boldsymbol{\mathrm{I}}\mathrm{cosh}\:\left({t}\right)+\boldsymbol{\mathrm{A}}\mathrm{sinh}\:\left({t}\right) \\ $$$$ \\ $$

Commented by BHOOPENDRA last updated on 17/May/21

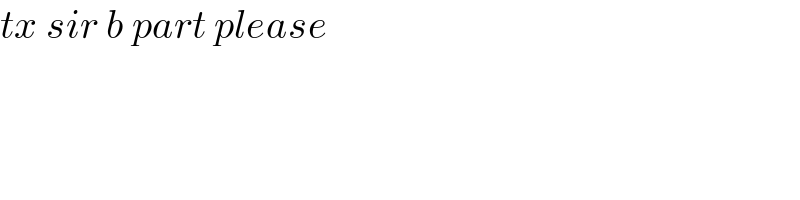
$${tx}\:{sir}\:{b}\:{part}\:{please} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply