Menu Close

Question-141352

Tinku Tara 0 Comments
Pin




Question Number 141352 by mathdanisur last updated on 17/May/21
Answered by Rasheed.Sindhi last updated on 18/May/21
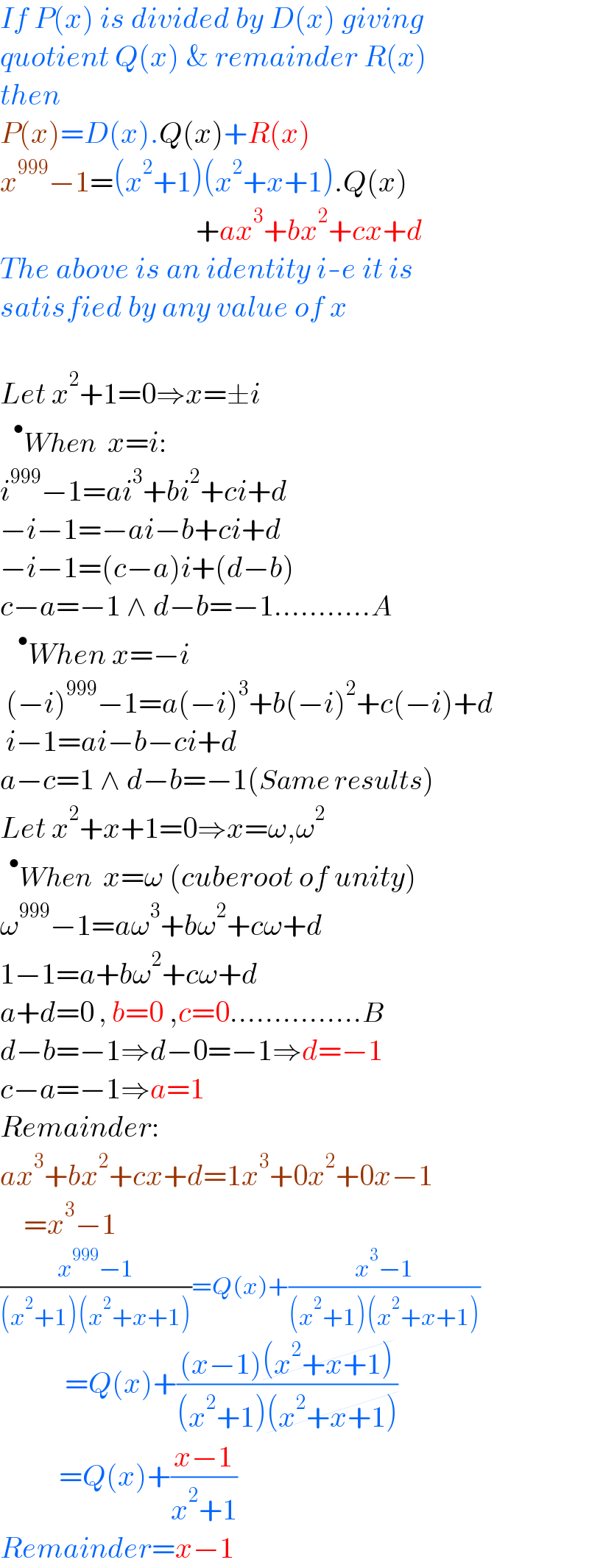
If P(x) is divided by D(x) giving quotient Q(x) & remainder R(x) then P(x)=D(x).Q(x)+R(x) x^(999) −1=(x^2 +1)(x^2 +x+1).Q(x) +ax^3 +bx^2 +cx+d The above is an identity i-e it is satisfied by any value of x Let x^2 +1=0⇒x=±i ^• When x=i: i^(999) −1=ai^3 +bi^2 +ci+d −i−1=−ai−b+ci+d −i−1=(c−a)i+(d−b) c−a=−1 ∧ d−b=−1...........A ^• When x=−i (−i)^(999) −1=a(−i)^3 +b(−i)^2 +c(−i)+d i−1=ai−b−ci+d a−c=1 ∧ d−b=−1(Same results) Let x^2 +x+1=0⇒x=ω,ω^2 ^• When x=ω (cuberoot of unity) ω^(999) −1=aω^3 +bω^2 +cω+d 1−1=a+bω^2 +cω+d a+d=0 , b=0 ,c=0...............B d−b=−1⇒d−0=−1⇒d=−1 c−a=−1⇒a=1 Remainder: ax^3 +bx^2 +cx+d=1x^3 +0x^2 +0x−1 =x^3 −1 ((x^(999) −1)/((x^2 +1)(x^2 +x+1)))=Q(x)+((x^3 −1)/((x^2 +1)(x^2 +x+1))) =Q(x)+(((x−1)(x^2 +x+1))/((x^2 +1)(x^2 +x+1))) =Q(x)+((x−1)/(x^2 +1)) Remainder=x−1
$${If}\:{P}\left({x}\right)\:{is}\:{divided}\:{by}\:{D}\left({x}\right)\:{giving} \\ $$$${quotient}\:{Q}\left({x}\right)\:\&\:{remainder}\:{R}\left({x}\right) \\ $$$${then} \\ $$$${P}\left({x}\right)={D}\left({x}\right).{Q}\left({x}\right)+{R}\left({x}\right) \\ $$$${x}^{\mathrm{999}} −\mathrm{1}=\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right).{Q}\left({x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$${The}\:{above}\:{is}\:{an}\:{identity}\:{i}-{e}\:{it}\:{is} \\ $$$${satisfied}\:{by}\:{any}\:{value}\:{of}\:{x} \\ $$$$ \\ $$$${Let}\:{x}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\Rightarrow{x}=\pm{i} \\ $$$$\:\:\:^{\bullet} {When}\:\:{x}={i}: \\ $$$${i}^{\mathrm{999}} −\mathrm{1}={ai}^{\mathrm{3}} +{bi}^{\mathrm{2}} +{ci}+{d} \\ $$$$−{i}−\mathrm{1}=−{ai}−{b}+{ci}+{d} \\ $$$$−{i}−\mathrm{1}=\left({c}−{a}\right){i}+\left({d}−{b}\right) \\ $$$${c}−{a}=−\mathrm{1}\:\wedge\:{d}−{b}=−\mathrm{1}………..{A} \\ $$$$\:\:\:^{\bullet} {When}\:{x}=−{i} \\ $$$$\:\left(−{i}\right)^{\mathrm{999}} −\mathrm{1}={a}\left(−{i}\right)^{\mathrm{3}} +{b}\left(−{i}\right)^{\mathrm{2}} +{c}\left(−{i}\right)+{d} \\ $$$$\:{i}−\mathrm{1}={ai}−{b}−{ci}+{d} \\ $$$${a}−{c}=\mathrm{1}\:\wedge\:{d}−{b}=−\mathrm{1}\left({Same}\:{results}\right) \\ $$$${Let}\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\omega,\omega^{\mathrm{2}} \\ $$$$\:\:^{\bullet} {When}\:\:{x}=\omega\:\left({cuberoot}\:{of}\:{unity}\right) \\ $$$$\omega^{\mathrm{999}} −\mathrm{1}={a}\omega^{\mathrm{3}} +{b}\omega^{\mathrm{2}} +{c}\omega+{d} \\ $$$$\mathrm{1}−\mathrm{1}={a}+{b}\omega^{\mathrm{2}} +{c}\omega+{d} \\ $$$${a}+{d}=\mathrm{0}\:,\:{b}=\mathrm{0}\:,{c}=\mathrm{0}……………{B} \\ $$$${d}−{b}=−\mathrm{1}\Rightarrow{d}−\mathrm{0}=−\mathrm{1}\Rightarrow{d}=−\mathrm{1} \\ $$$${c}−{a}=−\mathrm{1}\Rightarrow{a}=\mathrm{1} \\ $$$${Remainder}:\: \\ $$$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{1}{x}^{\mathrm{3}} +\mathrm{0}{x}^{\mathrm{2}} +\mathrm{0}{x}−\mathrm{1} \\ $$$$\:\:\:\:={x}^{\mathrm{3}} −\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{999}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}={Q}\left({x}\right)+\frac{{x}^{\mathrm{3}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={Q}\left({x}\right)+\frac{\left({x}−\mathrm{1}\right)\cancel{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\cancel{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}} \\ $$$$\:\:\:\:\:\:\:\:\:\:={Q}\left({x}\right)+\frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${Remainder}={x}−\mathrm{1} \\ $$
Commented by mathdanisur last updated on 18/May/21
cool dear Sir thankyou
$${cool}\:{dear}\:{Sir}\:{thankyou} \\ $$
Commented by mathdanisur last updated on 18/May/21
Sir, ans: x−1
$${Sir},\:{ans}:\:{x}−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *