Question Number 141373 by SLVR last updated on 18/May/21
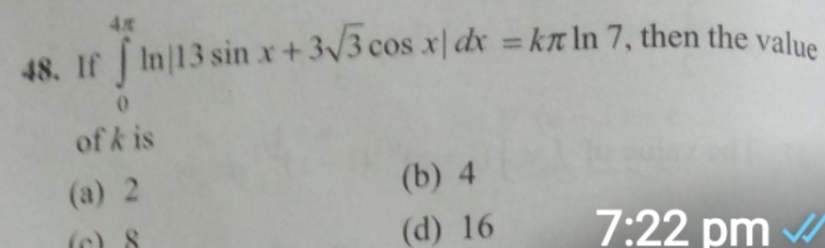
Commented by SLVR last updated on 18/May/21

$${kindly}\:{help}\:{me} \\ $$
Answered by mathmax by abdo last updated on 19/May/21

$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{4}\pi} \mathrm{log}\mid\mathrm{13sinx}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{cosx}\mid\:\mathrm{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{log}\mid\mathrm{13sinx}\:+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{cosx}\mid\mathrm{dx} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{log}\mid\mathrm{13sinx}\:+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{cosx}\:+\mathrm{a}\mid\mathrm{dx}\:\:\Rightarrow\mathrm{f}\left(\mathrm{0}\right)=\mathrm{I} \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{13sinx}\:+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{cosx}}\:=_{\mathrm{e}^{\mathrm{ix}} =\mathrm{z}} \:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{13}\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2i}}+\mathrm{3}\sqrt{\mathrm{3}}.\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\frac{\mathrm{13}\left(\mathrm{z}−\mathrm{z}^{−\mathrm{1}} \right)}{\mathrm{2i}}+\frac{\mathrm{i3}\sqrt{\mathrm{3}}\left(\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \right)}{\mathrm{2i}}\right)} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2dz}}{\mathrm{13}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2dz}}{\left(\mathrm{13}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}\right)\mathrm{z}^{\mathrm{2}} −\mathrm{13}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{13}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}}\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} −\frac{\mathrm{13}−\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{13}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{13}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} −\frac{\left(\mathrm{13}−\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{13}^{\mathrm{2}} \:+\mathrm{27}}} \\ $$$$….\mathrm{be}\:\mathrm{continued}…. \\ $$
