Question Number 141533 by sarkor last updated on 20/May/21

Answered by qaz last updated on 20/May/21
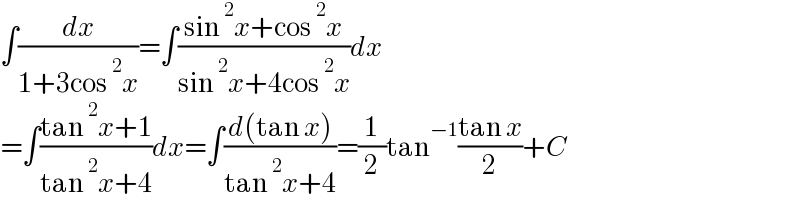
$$\int\frac{{dx}}{\mathrm{1}+\mathrm{3cos}\:^{\mathrm{2}} {x}}=\int\frac{\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} {x}}{\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{4cos}\:^{\mathrm{2}} {x}}{dx} \\ $$$$=\int\frac{\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{4}}{dx}=\int\frac{{d}\left(\mathrm{tan}\:{x}\right)}{\mathrm{tan}\:^{\mathrm{2}} {x}+\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:{x}}{\mathrm{2}}+{C} \\ $$
Commented by Mathspace last updated on 20/May/21

$$\Psi=\int\:\:\frac{{dx}}{\mathrm{1}+\mathrm{3}{cos}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$$\Psi=\int\:\:\frac{{dx}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)\right)} \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\int\:\:\frac{{dt}}{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}+{cost}\right)\right)} \\ $$$$=\int\:\:\frac{{dt}}{\mathrm{2}+\mathrm{3}+\mathrm{3}{cost}}\:=\int\:\frac{{dt}}{\mathrm{5}+\mathrm{3}{cost}} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={y}} \:\:\int\:\:\frac{\mathrm{2}{dy}}{\left(\mathrm{1}+{y}^{\mathrm{2}} \right)\left(\mathrm{5}+\mathrm{3}\frac{\mathrm{1}−{y}^{\mathrm{2}} }{\mathrm{1}+{y}^{\mathrm{2}} }\right)} \\ $$$$=\int\:\:\frac{\mathrm{2}{dy}}{\mathrm{5}+\mathrm{5}{y}^{\mathrm{2}} \:+\mathrm{3}−\mathrm{3}{y}^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{2}{dy}}{\mathrm{8}+\mathrm{2}{y}^{\mathrm{2}} }\:=\int\:\frac{{dy}}{\mathrm{4}+{y}^{\mathrm{2}} }\:=_{{y}=\mathrm{2}{z}} \\ $$$$=\int\:\frac{\mathrm{2}{dz}}{\mathrm{4}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({z}\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{{y}}{\mathrm{2}}\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}{tan}\left({x}\right)\right)\:+{C} \\ $$
