Question Number 141627 by cherokeesay last updated on 21/May/21

Answered by MJS_new last updated on 21/May/21
![((sin 2x +sin 4x)/(1+cos 2x +cos 4x))=((−2sin x cos x (1−4cos^2 x))/(1+2cos^2 x (1−4sin^2 x)))= [sin x =((tan x)/( (√(1+tan^2 x))))∧cos x =(1/( (√(1+tan^2 x))))] =((2tan x)/(1−tan^2 x)) ⇒ lim_(x→(π/3)) ((sin 2x +sin 4x)/(1+cos 2x +cos 4x)) =lim_(x→(π/3)) ((2tan x)/(1−tan^2 x)) =−(√3)](https://www.tinkutara.com/question/Q141634.png)
$$\frac{\mathrm{sin}\:\mathrm{2}{x}\:+\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{cos}\:\mathrm{4}{x}}=\frac{−\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x}\:\left(\mathrm{1}−\mathrm{4cos}^{\mathrm{2}} \:{x}\right)}{\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{x}\:\left(\mathrm{1}−\mathrm{4sin}^{\mathrm{2}} \:{x}\right)}= \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:{x}\:=\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}}\wedge\mathrm{cos}\:{x}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}}\right] \\ $$$$=\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}} \\ $$$$\Rightarrow \\ $$$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}\:+\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{cos}\:\mathrm{4}{x}}\:=\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {\mathrm{lim}}\:\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:{x}}\:=−\sqrt{\mathrm{3}} \\ $$
Commented by cherokeesay last updated on 21/May/21

$${thank}\:{you}\:{sir}. \\ $$
Commented by MJS_new last updated on 21/May/21

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
Answered by bramlexs22 last updated on 22/May/21
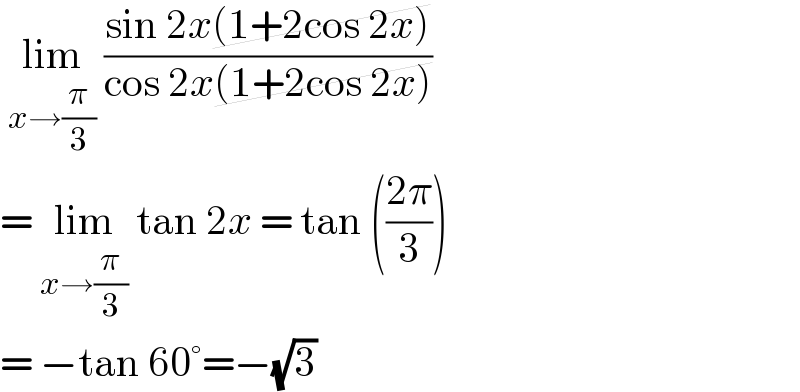
$$\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{2}{x}\cancel{\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{2}{x}\right)}}{\mathrm{cos}\:\mathrm{2}{x}\cancel{\left(\mathrm{1}+\mathrm{2cos}\:\mathrm{2}{x}\right)}} \\ $$$$=\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {\mathrm{lim}}\:\mathrm{tan}\:\mathrm{2}{x}\:=\:\mathrm{tan}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$=\:−\mathrm{tan}\:\mathrm{60}°=−\sqrt{\mathrm{3}} \\ $$
