Question Number 141643 by Gbenga last updated on 21/May/21
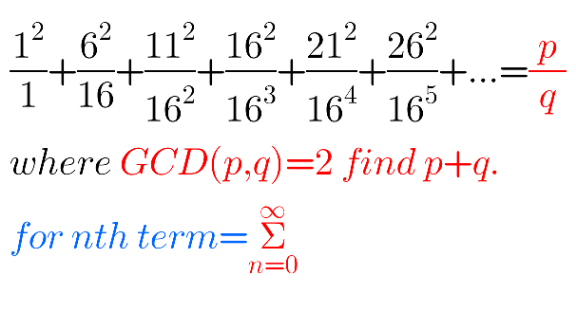
Answered by qaz last updated on 22/May/21
![S=Σ_(n=0) ^∞ (((5n+1)^2 )/(16^n )) =(5xD+1)^2 ∣_(x=1/16) Σ_(n=0) ^∞ x^n =[25(xD)^2 +10xD+1]_(x=1/16) (1/(1−x)) =[25x^2 D^2 +35xD+1]_(x=1/16) (1/(1−x))...................(xD)^2 =x^2 D^2 +xD =[((50x^2 )/((1−x)^3 ))+((35x)/((1−x)^2 ))+(1/(1−x))]_(x=1/16) =((50×16)/(15^3 ))+((35×16)/(15^2 ))+((16)/(15)) =((512)/(135))](https://www.tinkutara.com/question/Q141683.png)
$${S}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{5}{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{16}^{{n}} } \\ $$$$=\left(\mathrm{5}{xD}+\mathrm{1}\right)^{\mathrm{2}} \mid_{{x}=\mathrm{1}/\mathrm{16}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \\ $$$$=\left[\mathrm{25}\left({xD}\right)^{\mathrm{2}} +\mathrm{10}{xD}+\mathrm{1}\right]_{{x}=\mathrm{1}/\mathrm{16}} \frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\left[\mathrm{25}{x}^{\mathrm{2}} {D}^{\mathrm{2}} +\mathrm{35}{xD}+\mathrm{1}\right]_{{x}=\mathrm{1}/\mathrm{16}} \frac{\mathrm{1}}{\mathrm{1}−{x}}……………….\left({xD}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} {D}^{\mathrm{2}} +{xD} \\ $$$$=\left[\frac{\mathrm{50}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }+\frac{\mathrm{35}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{1}−{x}}\right]_{{x}=\mathrm{1}/\mathrm{16}} \\ $$$$=\frac{\mathrm{50}×\mathrm{16}}{\mathrm{15}^{\mathrm{3}} }+\frac{\mathrm{35}×\mathrm{16}}{\mathrm{15}^{\mathrm{2}} }+\frac{\mathrm{16}}{\mathrm{15}} \\ $$$$=\frac{\mathrm{512}}{\mathrm{135}} \\ $$
