Question Number 141669 by bramlexs22 last updated on 22/May/21

Answered by iloveisrael last updated on 22/May/21
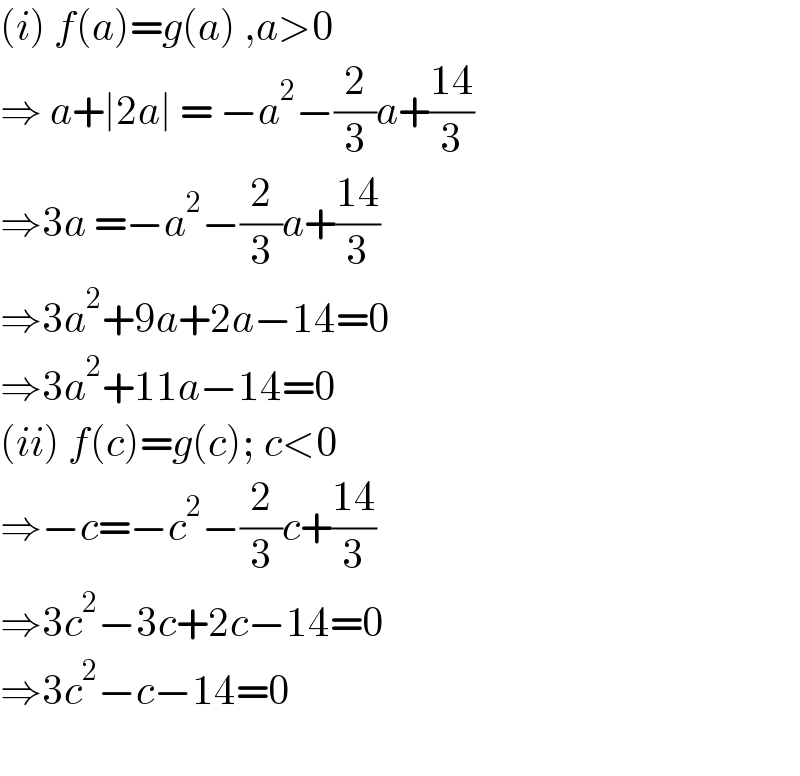
$$\left({i}\right)\:{f}\left({a}\right)={g}\left({a}\right)\:,{a}>\mathrm{0} \\ $$$$\Rightarrow\:{a}+\mid\mathrm{2}{a}\mid\:=\:−{a}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{a}+\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}{a}\:=−{a}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{a}+\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}{a}^{\mathrm{2}} +\mathrm{9}{a}+\mathrm{2}{a}−\mathrm{14}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}{a}^{\mathrm{2}} +\mathrm{11}{a}−\mathrm{14}=\mathrm{0} \\ $$$$\left({ii}\right)\:{f}\left({c}\right)={g}\left({c}\right);\:{c}<\mathrm{0} \\ $$$$\Rightarrow−{c}=−{c}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{3}}{c}+\frac{\mathrm{14}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}{c}^{\mathrm{2}} −\mathrm{3}{c}+\mathrm{2}{c}−\mathrm{14}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}{c}^{\mathrm{2}} −{c}−\mathrm{14}=\mathrm{0} \\ $$$$ \\ $$
