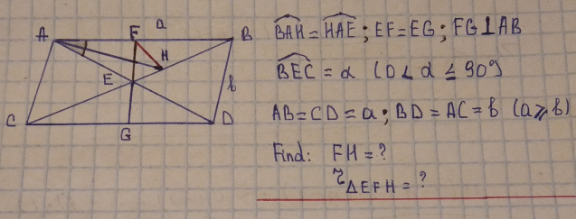
Question Number 141812 by mathsuji last updated on 23/May/21
Commented by mr W last updated on 23/May/21

$${check}\:{your}\:{question}\:{and}\:{diagram}! \\ $$$$\angle{BEC}=\alpha\:? \\ $$$${but}\:{according}\:{to}\:{diagram} \\ $$$$\angle{BEC}=\mathrm{180}° \\ $$
Commented by mathsuji last updated on 23/May/21

$${Sorry}\:{sir},\:{BED}=\alpha \\ $$
Answered by mr W last updated on 24/May/21

Commented by mr W last updated on 24/May/21
![given: a,b,α let p=EB, q=EA, ∠EAB=β b^2 =p^2 +q^2 −2pqcos α a^2 =p^2 +q^2 +2pqcos α if α=90°: p=q=((√(a^2 +b^2 ))/2) otherwise: ⇒pq=((a^2 −b^2 )/(4cos α))=μ, say ⇒p^2 +q^2 =((a^2 +b^2 )/2)=λ, say ⇒p^4 +q^2 p^2 =λp^2 ⇒p^4 −λp^2 +μ^2 =0 ⇒p^2 =((λ±(√(λ^2 −4μ^2 )))/2) ⇒p=(√((λ+(√(λ^2 −4μ^2 )))/2)) ⇒q=(√((λ−(√(λ^2 −4μ^2 )))/2)) ((sin β)/p)=((sin α)/a) ⇒sin β=((p sin α)/a) ⇒β=sin^(−1) (((p sin α)/a)) EF=q sin β=((pq sin α)/a)=(((a^2 −b^2 )tan α)/(4a)) ((EH)/(sin (β/2)))=(q/(sin α)) ⇒EH=((q sin (β/2))/(sin α)) A_(ΔEFH) =((EF×EH×sin ((π/2)−α+β))/2) ⇒A_(ΔEFH) =(((a^2 −b^2 )q sin (β/2) cos (α−β))/(8a cos α)) FH^2 =EF^2 +EH^2 −2×EF×EH×cos ((π/2)−α+β) ⇒EH=(√([(((a^2 −b^2 )tan α)/(4a))]^2 +[((q sin (β/2))/(sin α))]^2 −(((a^2 −b^2 )q sin (β/2)sin (α−β))/(2acos α))))](https://www.tinkutara.com/question/Q141857.png)
$${given}:\:{a},{b},\alpha \\ $$$${let}\:{p}={EB},\:{q}={EA},\:\angle{EAB}=\beta \\ $$$${b}^{\mathrm{2}} ={p}^{\mathrm{2}} +{q}^{\mathrm{2}} −\mathrm{2}{pq}\mathrm{cos}\:\alpha \\ $$$${a}^{\mathrm{2}} ={p}^{\mathrm{2}} +{q}^{\mathrm{2}} +\mathrm{2}{pq}\mathrm{cos}\:\alpha \\ $$$${if}\:\alpha=\mathrm{90}°:\:{p}={q}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${otherwise}: \\ $$$$\Rightarrow{pq}=\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{4cos}\:\alpha}=\mu,\:{say} \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}=\lambda,\:{say} \\ $$$$\Rightarrow{p}^{\mathrm{4}} +{q}^{\mathrm{2}} {p}^{\mathrm{2}} =\lambda{p}^{\mathrm{2}} \\ $$$$\Rightarrow{p}^{\mathrm{4}} −\lambda{p}^{\mathrm{2}} +\mu^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\frac{\lambda\pm\sqrt{\lambda^{\mathrm{2}} −\mathrm{4}\mu^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\Rightarrow{p}=\sqrt{\frac{\lambda+\sqrt{\lambda^{\mathrm{2}} −\mathrm{4}\mu^{\mathrm{2}} }}{\mathrm{2}}} \\ $$$$\Rightarrow{q}=\sqrt{\frac{\lambda−\sqrt{\lambda^{\mathrm{2}} −\mathrm{4}\mu^{\mathrm{2}} }}{\mathrm{2}}} \\ $$$$\frac{\mathrm{sin}\:\beta}{{p}}=\frac{\mathrm{sin}\:\alpha}{{a}} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{{p}\:\mathrm{sin}\:\alpha}{{a}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \left(\frac{{p}\:\mathrm{sin}\:\alpha}{{a}}\right) \\ $$$${EF}={q}\:\mathrm{sin}\:\beta=\frac{{pq}\:\mathrm{sin}\:\alpha}{{a}}=\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{tan}\:\alpha}{\mathrm{4}{a}} \\ $$$$\frac{{EH}}{\mathrm{sin}\:\frac{\beta}{\mathrm{2}}}=\frac{{q}}{\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow{EH}=\frac{{q}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}}{\mathrm{sin}\:\alpha} \\ $$$${A}_{\Delta{EFH}} =\frac{{EF}×{EH}×\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\alpha+\beta\right)}{\mathrm{2}} \\ $$$$\Rightarrow{A}_{\Delta{EFH}} =\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){q}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\left(\alpha−\beta\right)}{\mathrm{8}{a}\:\mathrm{cos}\:\alpha} \\ $$$${FH}^{\mathrm{2}} ={EF}^{\mathrm{2}} +{EH}^{\mathrm{2}} −\mathrm{2}×{EF}×{EH}×\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\alpha+\beta\right) \\ $$$$\Rightarrow{EH}=\sqrt{\left[\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{tan}\:\alpha}{\mathrm{4}{a}}\right]^{\mathrm{2}} +\left[\frac{{q}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}}{\mathrm{sin}\:\alpha}\right]^{\mathrm{2}} −\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){q}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}\mathrm{sin}\:\left(\alpha−\beta\right)}{\mathrm{2}{a}\mathrm{cos}\:\alpha}} \\ $$
