Question-141822

Question Number 141822 by mathsuji last updated on 23/May/21

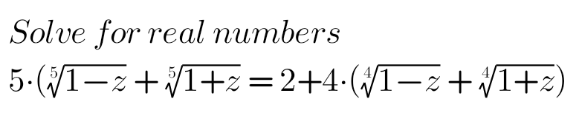
Commented by MJS_new last updated on 23/May/21

where you found this? did your teacher gave it to you? which chapter of solving equations are you studying? have you got any idea? • yes: then please tell us • no: then believe me, there′s no general method to solve it. I can see z=0 solves it. can you see anything else?

$$\mathrm{where}\:\mathrm{you}\:\mathrm{found}\:\mathrm{this}? \\ $$$$\mathrm{did}\:\mathrm{your}\:\mathrm{teacher}\:\mathrm{gave}\:\mathrm{it}\:\mathrm{to}\:\mathrm{you}?\:\mathrm{which}\:\mathrm{chapter} \\ $$$$\mathrm{of}\:\mathrm{solving}\:\mathrm{equations}\:\mathrm{are}\:\mathrm{you}\:\mathrm{studying}? \\ $$$$\mathrm{have}\:\mathrm{you}\:\mathrm{got}\:\mathrm{any}\:\mathrm{idea}? \\ $$$$\bullet\:\mathrm{yes}:\:\mathrm{then}\:\mathrm{please}\:\mathrm{tell}\:\mathrm{us} \\ $$$$\bullet\:\mathrm{no}:\:\mathrm{then}\:\mathrm{believe}\:\mathrm{me},\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{general} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{method}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}. \\ $$$$\mathrm{I}\:\mathrm{can}\:\mathrm{see}\:{z}=\mathrm{0}\:\mathrm{solves}\:\mathrm{it}.\:\mathrm{can}\:\mathrm{you}\:\mathrm{see}\:\mathrm{anything} \\ $$$$\mathrm{else}? \\ $$

Commented by mathdanisur last updated on 23/May/21

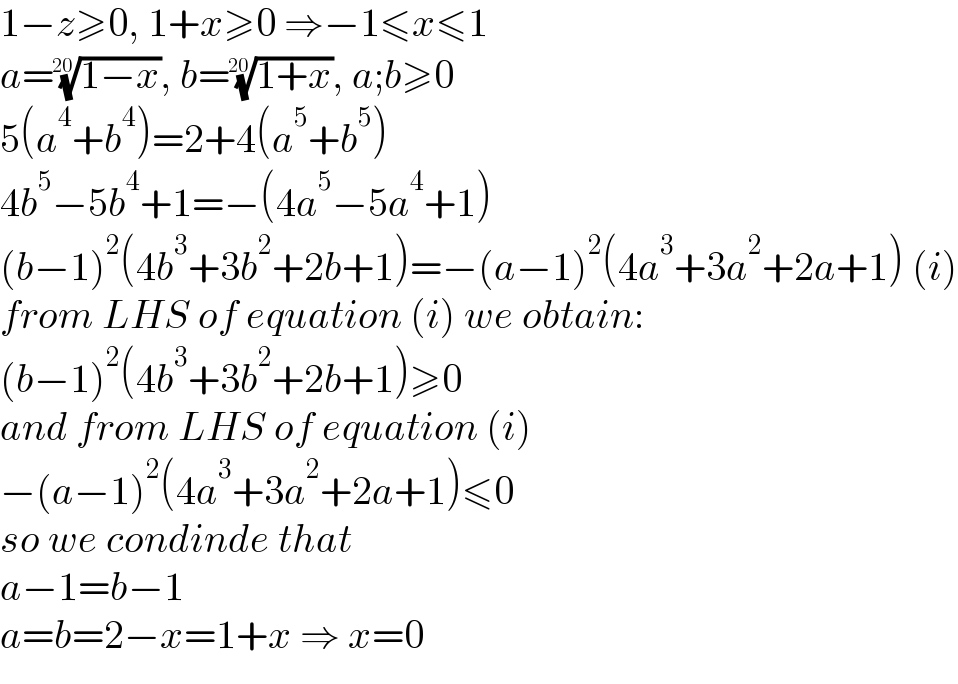
1−z≥0, 1+x≥0 ⇒−1≤x≤1 a=((1−x))^(1/(20)) , b=((1+x))^(1/(20)) , a;b≥0 5(a^4 +b^4 )=2+4(a^5 +b^5 ) 4b^5 −5b^4 +1=−(4a^5 −5a^4 +1) (b−1)^2 (4b^3 +3b^2 +2b+1)=−(a−1)^2 (4a^3 +3a^2 +2a+1) (i) from LHS of equation (i) we obtain: (b−1)^2 (4b^3 +3b^2 +2b+1)≥0 and from LHS of equation (i) −(a−1)^2 (4a^3 +3a^2 +2a+1)≤0 so we condinde that a−1=b−1 a=b=2−x=1+x ⇒ x=0

$$\mathrm{1}−{z}\geqslant\mathrm{0},\:\mathrm{1}+{x}\geqslant\mathrm{0}\:\Rightarrow−\mathrm{1}\leqslant{x}\leqslant\mathrm{1} \\ $$$${a}=\sqrt[{\mathrm{20}}]{\mathrm{1}−{x}},\:{b}=\sqrt[{\mathrm{20}}]{\mathrm{1}+{x}},\:{a};{b}\geqslant\mathrm{0} \\ $$$$\mathrm{5}\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)=\mathrm{2}+\mathrm{4}\left({a}^{\mathrm{5}} +{b}^{\mathrm{5}} \right) \\ $$$$\mathrm{4}{b}^{\mathrm{5}} −\mathrm{5}{b}^{\mathrm{4}} +\mathrm{1}=−\left(\mathrm{4}{a}^{\mathrm{5}} −\mathrm{5}{a}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$$\left({b}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4}{b}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\right)=−\left({a}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}\right)\:\left({i}\right) \\ $$$${from}\:{LHS}\:{of}\:{equation}\:\left({i}\right)\:{we}\:{obtain}: \\ $$$$\left({b}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4}{b}^{\mathrm{3}} +\mathrm{3}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$${and}\:{from}\:{LHS}\:{of}\:{equation}\:\left({i}\right) \\ $$$$−\left({a}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{4}{a}^{\mathrm{3}} +\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}+\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$${so}\:{we}\:{condinde}\:{that} \\ $$$${a}−\mathrm{1}={b}−\mathrm{1} \\ $$$${a}={b}=\mathrm{2}−{x}=\mathrm{1}+{x}\:\Rightarrow\:{x}=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply