Question Number 141872 by mohammad17 last updated on 24/May/21

Commented by mohammad17 last updated on 24/May/21
$${help}\:{me}\:{sir}\:{please} \\ $$
Commented by mohammad17 last updated on 24/May/21

$$???? \\ $$
Answered by Dwaipayan Shikari last updated on 24/May/21
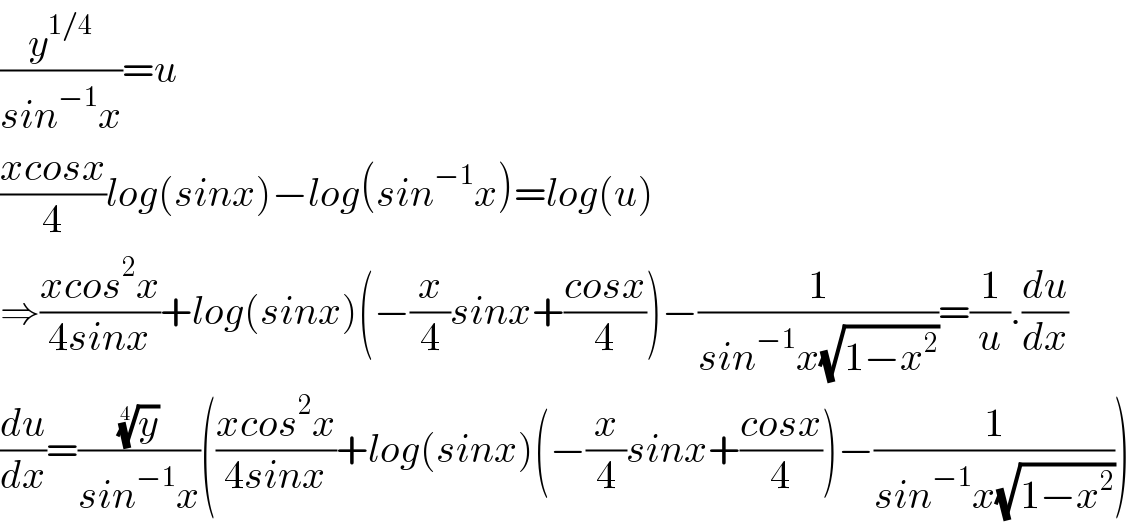
$$\frac{{y}^{\mathrm{1}/\mathrm{4}} }{{sin}^{−\mathrm{1}} {x}}={u} \\ $$$$\frac{{xcosx}}{\mathrm{4}}{log}\left({sinx}\right)−{log}\left({sin}^{−\mathrm{1}} {x}\right)={log}\left({u}\right) \\ $$$$\Rightarrow\frac{{xcos}^{\mathrm{2}} {x}}{\mathrm{4}{sinx}}+{log}\left({sinx}\right)\left(−\frac{{x}}{\mathrm{4}}{sinx}+\frac{{cosx}}{\mathrm{4}}\right)−\frac{\mathrm{1}}{{sin}^{−\mathrm{1}} {x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\frac{\mathrm{1}}{{u}}.\frac{{du}}{{dx}} \\ $$$$\frac{{du}}{{dx}}=\frac{\sqrt[{\mathrm{4}}]{{y}}}{{sin}^{−\mathrm{1}} {x}}\left(\frac{{xcos}^{\mathrm{2}} {x}}{\mathrm{4}{sinx}}+{log}\left({sinx}\right)\left(−\frac{{x}}{\mathrm{4}}{sinx}+\frac{{cosx}}{\mathrm{4}}\right)−\frac{\mathrm{1}}{{sin}^{−\mathrm{1}} {x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\right) \\ $$
Commented by mohammad17 last updated on 24/May/21

$${thank}\:{you}\:{sir} \\ $$
