Question Number 141909 by mathdanisur last updated on 24/May/21
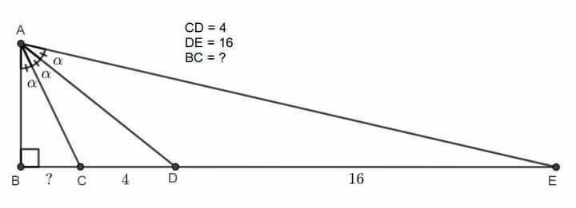
Commented by mr W last updated on 24/May/21

$${BC}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 24/May/21

$${AB}={h} \\ $$$${BC}={x} \\ $$$$\mathrm{tan}\:\alpha=\frac{{x}}{{h}} \\ $$$$\mathrm{tan}\:\mathrm{2}\alpha=\frac{{x}+\mathrm{4}}{{h}}=\frac{\mathrm{2}×\frac{{x}}{{h}}}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{h}^{\mathrm{2}} }} \\ $$$$\Rightarrow{h}^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{4}\right)}{\mathrm{4}−{x}} \\ $$$$\mathrm{tan}\:\mathrm{3}\alpha=\frac{{x}+\mathrm{20}}{{h}}=\frac{\frac{{x}}{{h}}\left(\mathrm{3}−\frac{{x}^{\mathrm{2}} }{{h}^{\mathrm{2}} }\right)}{\mathrm{1}−\mathrm{3}×\frac{{x}^{\mathrm{2}} }{{h}^{\mathrm{2}} }} \\ $$$$\Rightarrow{h}^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{30}\right)}{\mathrm{10}−{x}} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{30}\right)}{\mathrm{10}−{x}}=\frac{{x}^{\mathrm{2}} \left({x}+\mathrm{4}\right)}{\mathrm{4}−{x}} \\ $$$$\Rightarrow\frac{{x}+\mathrm{30}}{\mathrm{10}−{x}}=\frac{{x}+\mathrm{4}}{\mathrm{4}−{x}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 25/May/21

$${cool}\:{Sir}\:{thanks} \\ $$
