Question Number 142025 by mnjuly1970 last updated on 25/May/21

Answered by som(math1967) last updated on 25/May/21
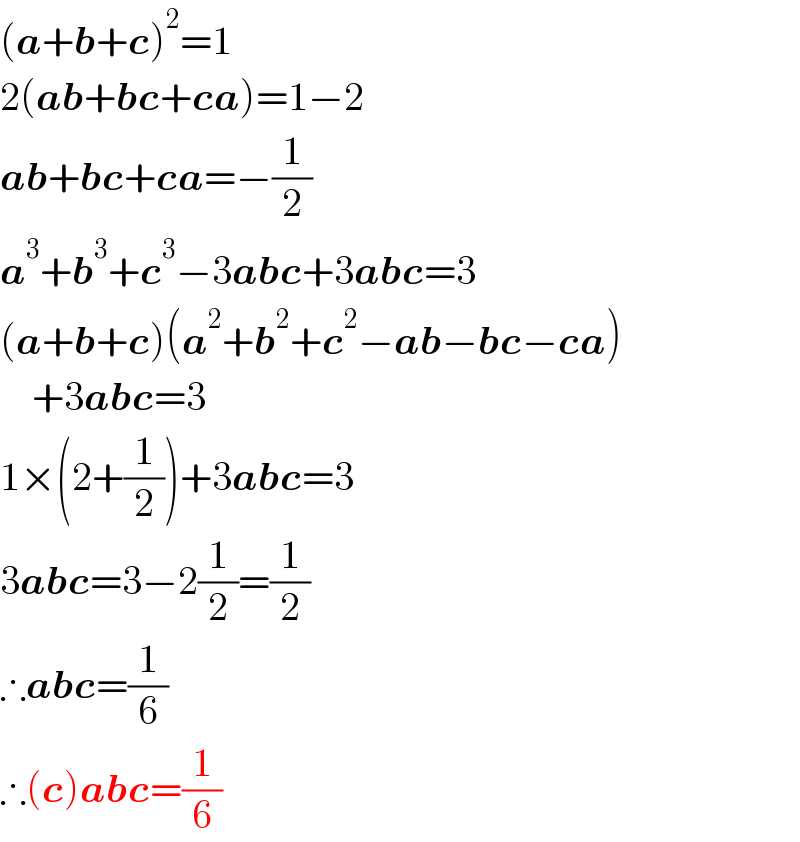
$$\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2}\left(\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ca}}\right)=\mathrm{1}−\mathrm{2} \\ $$$$\boldsymbol{{ab}}+\boldsymbol{{bc}}+\boldsymbol{{ca}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{a}}^{\mathrm{3}} +\boldsymbol{{b}}^{\mathrm{3}} +\boldsymbol{{c}}^{\mathrm{3}} −\mathrm{3}\boldsymbol{{abc}}+\mathrm{3}\boldsymbol{{abc}}=\mathrm{3} \\ $$$$\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)\left(\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} −\boldsymbol{{ab}}−\boldsymbol{{bc}}−\boldsymbol{{ca}}\right) \\ $$$$\:\:\:\:+\mathrm{3}\boldsymbol{{abc}}=\mathrm{3} \\ $$$$\mathrm{1}×\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3}\boldsymbol{{abc}}=\mathrm{3} \\ $$$$\mathrm{3}\boldsymbol{{abc}}=\mathrm{3}−\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\therefore\boldsymbol{{abc}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\therefore\left(\boldsymbol{{c}}\right)\boldsymbol{{abc}}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Commented by mnjuly1970 last updated on 25/May/21
$${thank}\:{you}\:{sir}\:{Som}… \\ $$
