Question Number 142045 by Engr_Jidda last updated on 25/May/21

Answered by Dwaipayan Shikari last updated on 25/May/21
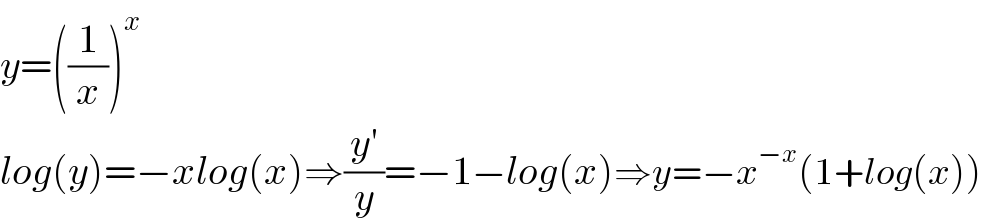
$${y}=\left(\frac{\mathrm{1}}{{x}}\right)^{{x}} \\ $$$${log}\left({y}\right)=−{xlog}\left({x}\right)\Rightarrow\frac{{y}'}{{y}}=−\mathrm{1}−{log}\left({x}\right)\Rightarrow{y}=−{x}^{−{x}} \left(\mathrm{1}+{log}\left({x}\right)\right) \\ $$
Commented by Engr_Jidda last updated on 25/May/21

$${thanks} \\ $$
Answered by EDWIN88 last updated on 26/May/21

$$\left(\mathrm{1}\right)\:\mathrm{y}=\mathrm{log}\:\left(\mathrm{cos}\:\mathrm{x}\right)\:\Rightarrow\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{e}^{\mathrm{y}} \\ $$$$\Rightarrow\:−\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{e}^{\mathrm{y}} .\:\mathrm{y}' \\ $$$$\Rightarrow\mathrm{y}'=−\mathrm{sin}\:\mathrm{x}.\mathrm{e}^{−\mathrm{y}} \:=\:−\mathrm{sin}\:\mathrm{x}.\mathrm{e}^{−\mathrm{log}\:\left(\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$\Rightarrow\mathrm{y}'=−\mathrm{sin}\:\mathrm{x}.\mathrm{sec}\:\mathrm{x}\: \\ $$
