Question Number 142060 by iloveisrael last updated on 26/May/21

Answered by Ar Brandon last updated on 26/May/21
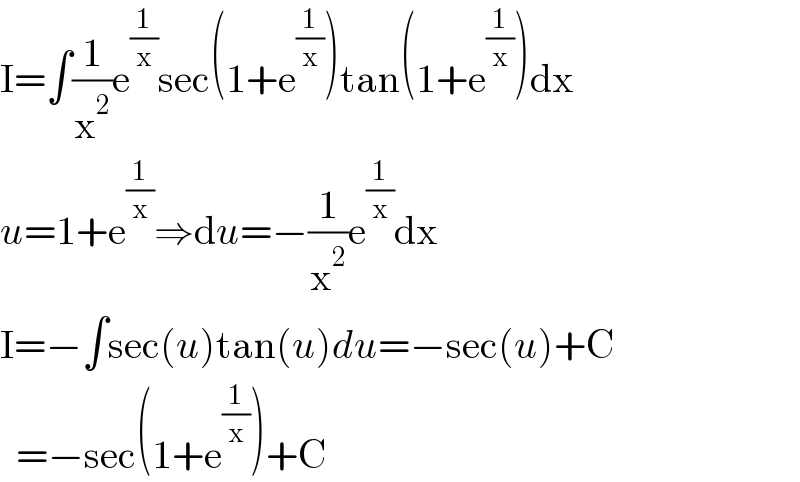
$$\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \mathrm{sec}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)\mathrm{tan}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)\mathrm{dx} \\ $$$${u}=\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \Rightarrow\mathrm{d}{u}=−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \mathrm{dx} \\ $$$$\mathrm{I}=−\int\mathrm{sec}\left({u}\right)\mathrm{tan}\left({u}\right){du}=−\mathrm{sec}\left({u}\right)+\mathrm{C} \\ $$$$\:\:=−\mathrm{sec}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)+\mathrm{C} \\ $$
Answered by EDWIN88 last updated on 26/May/21
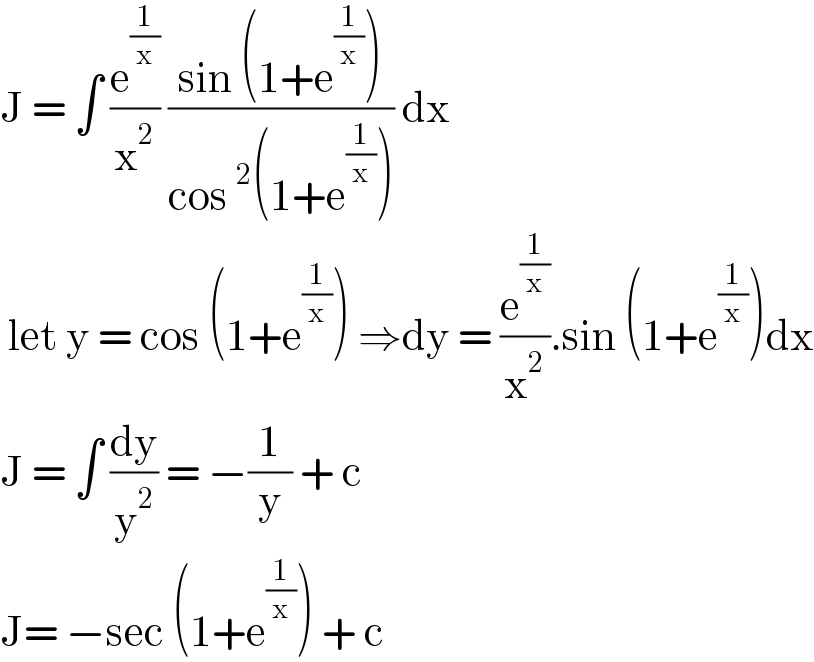
$$\mathrm{J}\:=\:\int\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{x}^{\mathrm{2}} }\:\frac{\mathrm{sin}\:\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)}{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)}\:\mathrm{dx} \\ $$$$\:\mathrm{let}\:\mathrm{y}\:=\:\mathrm{cos}\:\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)\:\Rightarrow\mathrm{dy}\:=\:\frac{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{x}^{\mathrm{2}} }.\mathrm{sin}\:\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)\mathrm{dx} \\ $$$$\mathrm{J}\:=\:\int\:\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{\mathrm{y}}\:+\:\mathrm{c}\: \\ $$$$\mathrm{J}=\:−\mathrm{sec}\:\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \right)\:+\:\mathrm{c}\: \\ $$
