Question Number 142205 by mohammad17 last updated on 27/May/21

Commented by mohammad17 last updated on 27/May/21

$${help}\:{me}\:{sir}\:? \\ $$
Commented by mohammad17 last updated on 27/May/21
$${yes}\:{sir}\:{can}\:{you}\:{help}\:{me}\:? \\ $$
Commented by mr W last updated on 27/May/21
$${he}\:{has}\:{helped}\:{you}! \\ $$$${what}\:{you}\:{still}\:{want}\:{is}\:{not}\:{called}\:{help}. \\ $$
Commented by liberty last updated on 28/May/21
![(1) y=(2/3)x^(3/2) ⇒y′= (√x) arc length = ∫_1 ^2 (√(1+((√x))^2 )) dx = ∫_1 ^2 (√(1+x)) d(1+x)= (2/3)[(√((1+x)^3 )) ]_1 ^2 = (2/3)((√(27))−(√8) )= (2/3)(3(√3)−2(√2))](https://www.tinkutara.com/question/Q142225.png)
$$\left(\mathrm{1}\right)\:{y}=\frac{\mathrm{2}}{\mathrm{3}}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \Rightarrow{y}'=\:\sqrt{{x}} \\ $$$$\:{arc}\:{length}\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\sqrt{\mathrm{1}+\left(\sqrt{{x}}\right)^{\mathrm{2}} }\:{dx} \\ $$$$\:=\:\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\sqrt{\mathrm{1}+{x}}\:{d}\left(\mathrm{1}+{x}\right)=\:\frac{\mathrm{2}}{\mathrm{3}}\left[\sqrt{\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }\:\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{\mathrm{27}}−\sqrt{\mathrm{8}}\:\right)=\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$
Commented by MJS_new last updated on 27/May/21
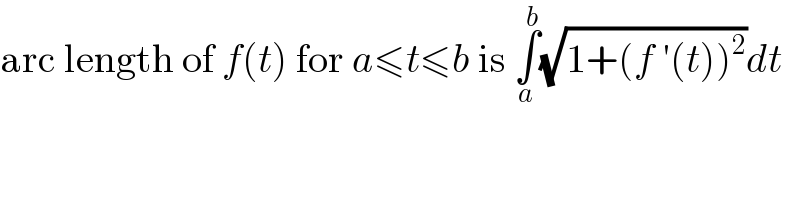
$$\mathrm{arc}\:\mathrm{length}\:\mathrm{of}\:{f}\left({t}\right)\:\mathrm{for}\:{a}\leqslant{t}\leqslant{b}\:\mathrm{is}\:\underset{{a}} {\overset{{b}} {\int}}\sqrt{\mathrm{1}+\left({f}\:'\left({t}\right)\right)^{\mathrm{2}} }{dt} \\ $$
