Question Number 142248 by gsk2684 last updated on 28/May/21
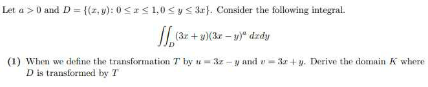
Commented by gsk2684 last updated on 31/May/21

$$\mathrm{let}\:\mathrm{a}>\mathrm{0}\:\mathrm{and} \\ $$$$\mathrm{D}=\left\{\left(\mathrm{x},\mathrm{y}\right)/\mathrm{0}\leq\mathrm{x}\leq\mathrm{1},\mathrm{0}\leq\mathrm{y}\leq\mathrm{3x}\right\} \\ $$$$\mathrm{consider}\:\mathrm{the}\:\mathrm{following}\:\mathrm{integral} \\ $$$$\int\underset{\mathrm{D}} {\int}\left(\mathrm{3x}+\mathrm{y}\right)\left(\mathrm{3x}−\mathrm{y}\right)^{\mathrm{a}} \mathrm{dxdy} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{when}\:\mathrm{we}\:\mathrm{define}\:\mathrm{the}\:\mathrm{transformation} \\ $$$$\mathrm{T}\:\mathrm{by}\:\mathrm{u}=\mathrm{3x}−\mathrm{y}\:\mathrm{and}\:\mathrm{v}=\mathrm{3x}+\mathrm{y} \\ $$$$\mathrm{Derive}\:\mathrm{the}\:\mathrm{domain}\:\mathrm{K}\:\mathrm{when}\:\mathrm{D}\: \\ $$$$\mathrm{is}\:\mathrm{transformed}\:\mathrm{by}\:\mathrm{T}. \\ $$$$ \\ $$
Commented by gsk2684 last updated on 28/May/21

$$\mathrm{solution}\:\mathrm{please} \\ $$
