Question Number 142253 by mathdave last updated on 28/May/21

Answered by mr W last updated on 28/May/21
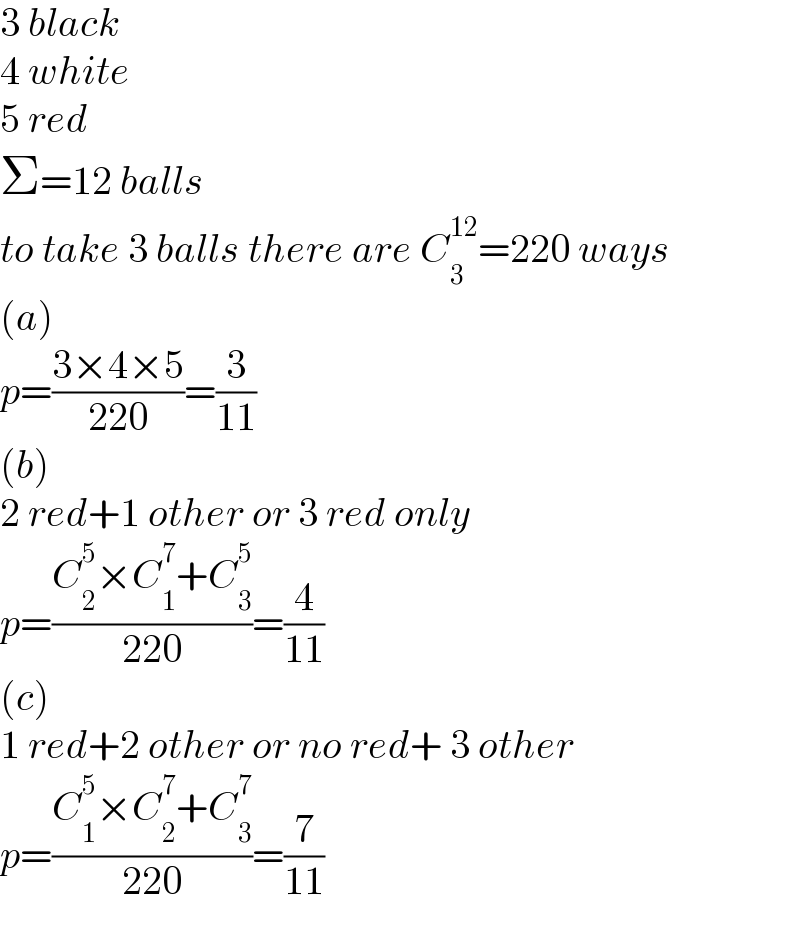
$$\mathrm{3}\:{black} \\ $$$$\mathrm{4}\:{white} \\ $$$$\mathrm{5}\:{red} \\ $$$$\Sigma=\mathrm{12}\:{balls} \\ $$$${to}\:{take}\:\mathrm{3}\:{balls}\:{there}\:{are}\:{C}_{\mathrm{3}} ^{\mathrm{12}} =\mathrm{220}\:{ways} \\ $$$$\left({a}\right) \\ $$$${p}=\frac{\mathrm{3}×\mathrm{4}×\mathrm{5}}{\mathrm{220}}=\frac{\mathrm{3}}{\mathrm{11}} \\ $$$$\left({b}\right) \\ $$$$\mathrm{2}\:{red}+\mathrm{1}\:{other}\:{or}\:\mathrm{3}\:{red}\:{only} \\ $$$${p}=\frac{{C}_{\mathrm{2}} ^{\mathrm{5}} ×{C}_{\mathrm{1}} ^{\mathrm{7}} +{C}_{\mathrm{3}} ^{\mathrm{5}} }{\mathrm{220}}=\frac{\mathrm{4}}{\mathrm{11}} \\ $$$$\left({c}\right) \\ $$$$\mathrm{1}\:{red}+\mathrm{2}\:{other}\:{or}\:{no}\:{red}+\:\mathrm{3}\:{other} \\ $$$${p}=\frac{{C}_{\mathrm{1}} ^{\mathrm{5}} ×{C}_{\mathrm{2}} ^{\mathrm{7}} +{C}_{\mathrm{3}} ^{\mathrm{7}} }{\mathrm{220}}=\frac{\mathrm{7}}{\mathrm{11}} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
