Question Number 142326 by bramlexs22 last updated on 30/May/21

Answered by EDWIN88 last updated on 30/May/21
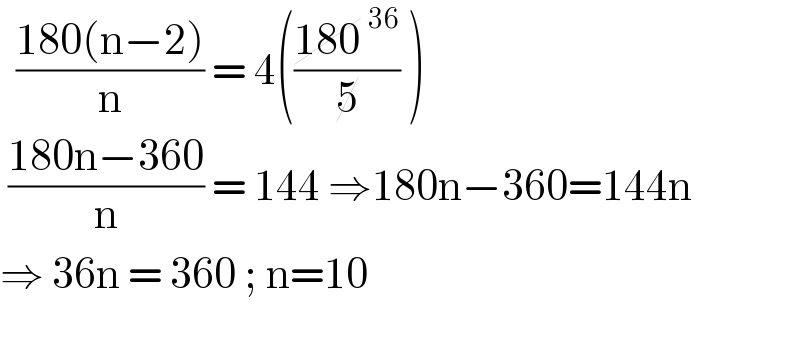
$$\:\:\frac{\mathrm{180}\left(\mathrm{n}−\mathrm{2}\right)}{\mathrm{n}}\:=\:\mathrm{4}\left(\frac{\cancel{\mathrm{180}}\:^{\mathrm{36}} }{\cancel{\mathrm{5}}}\:\right) \\ $$$$\:\frac{\mathrm{180n}−\mathrm{360}}{\mathrm{n}}\:=\:\mathrm{144}\:\Rightarrow\mathrm{180n}−\mathrm{360}=\mathrm{144n} \\ $$$$\Rightarrow\:\mathrm{36n}\:=\:\mathrm{360}\:;\:\mathrm{n}=\mathrm{10} \\ $$$$\: \\ $$
Answered by Rasheed.Sindhi last updated on 30/May/21

$${For}\:{n}-{gon} \\ $$$$\:^{\bullet} {Sum}\:{of}\:{interior}\:{angles}=\mathrm{180}\left({n}−\mathrm{2}\right) \\ $$$$\:^{\bullet} {Sum}\:{of}\:{exterior}\:{angles}=\mathrm{360}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\:{constant}\:{for}\:{all}\:{polygons}\right) \\ $$$$\mathrm{180}\left({n}−\mathrm{2}\right)=\mathrm{4}×\mathrm{360} \\ $$$$\mathrm{180}{n}=\mathrm{4}×\mathrm{360}+\mathrm{360}=\mathrm{5}×\mathrm{360} \\ $$$${n}=\frac{\mathrm{5}×\cancel{\overset{\mathrm{2}} {\mathrm{360}}}}{\cancel{\mathrm{180}}}=\mathrm{10} \\ $$
