Question Number 142401 by mohammad17 last updated on 31/May/21

Commented by mohammad17 last updated on 31/May/21
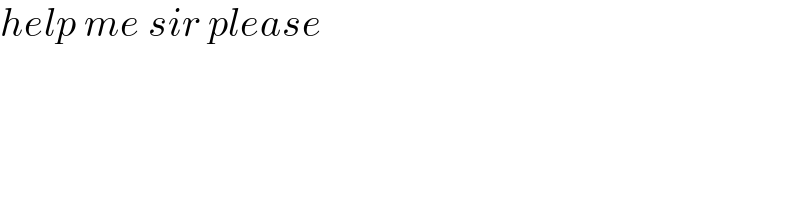
$${help}\:{me}\:{sir}\:{please} \\ $$
Answered by mr W last updated on 31/May/21

$${Q}\mathrm{1} \\ $$$${pressure}\:{at}\:{r}:\:{p}\left({r}\right) \\ $$$${r}=\mathrm{250}{mm}=\mathrm{0}.\mathrm{25}{m} \\ $$$${r}_{\mathrm{0}} ={r}−{t}=\mathrm{250}−\mathrm{120}=\mathrm{130}{mm}=\mathrm{0}.\mathrm{13}{m} \\ $$$${dp}=\rho{r}\omega^{\mathrm{2}} {dr} \\ $$$$\int_{\mathrm{0}} ^{{p}} {dp}=\int_{{r}_{\mathrm{0}} } ^{{r}} \rho{r}\omega^{\mathrm{2}} {dr} \\ $$$$\Rightarrow{p}=\frac{\rho\omega^{\mathrm{2}} \left({r}^{\mathrm{2}} −{r}_{\mathrm{0}} ^{\mathrm{2}} \right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2200}×\mathrm{160}^{\mathrm{2}} ×\left(\mathrm{0}.\mathrm{25}^{\mathrm{2}} −\mathrm{0}.\mathrm{13}^{\mathrm{2}} \right) \\ $$$$=\mathrm{1284096}\:{Pa}\approx\mathrm{1}.\mathrm{284}{MPa} \\ $$
