Menu Close

Question-142447

Tinku Tara 0 Comments
Pin




Question Number 142447 by ajfour last updated on 31/May/21
Commented by ajfour last updated on 31/May/21
Find ellipse perimeter.
$${Find}\:{ellipse}\:{perimeter}. \\ $$
Answered by Dwaipayan Shikari last updated on 31/May/21
(x^2 /a^2 )+(y^2 /b^2 )=1 ⇒y′=−((b^2 x)/(a^2 y))=−((bx)/(a(√(a^2 −x^2 )))) Perimetre =2∫_(−a) ^a (√(1+(y′)^2 )) dx =4∫_0 ^a (√(1+((b^2 x)/(a^2 (a^2 −x^2 ))))) dx x=ua =4∫_0 ^1 (1/a)(√((a^4 (1−u^2 )+a^2 b^2 u^2 )/(1−u^2 ))) du cosθ=u =4∫_0 ^(π/2) (√(a^2 sin^2 θ+b^2 cos^2 θ)) dθ =4a∫_0 ^(π/2) (√(1−(1−(b^2 /a^2 ))cos^2 θ)) dθ =4a∫_0 ^(π/2) (√(1−e^2 cos^2 θ)) dθ=4a∫_0 ^(π/2) (√(1−e^2 sin^2 θ)) dθ =4aE((π/2)∣e) Or 4a∫_0 ^(π/2) (√(1−e^2 sin^2 θ)) dθ=4aΣ_(n=0) ^∞ (((−(1/2))_n )/(n!))∫_0 ^(π/2) e^(2n) sin^(2n) θ dθ =2aΣ_(n=0) ^∞ (((−(1/2))_n e^(2n) )/(n!)).((Γ(n+(1/2))Γ((1/2)))/(Γ(n+1))) =2πaΣ_(n=0) ^∞ (((−(1/2))_n ((1/2))_n )/(n!(1)_n ))e^(2n) =2πa _2 F_1 (−(1/2),(1/2);1;e^2 )
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{y}'=−\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}}=−\frac{{bx}}{{a}\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$${Perimetre}\:=\mathrm{2}\int_{−{a}} ^{{a}} \sqrt{\mathrm{1}+\left({y}'\right)^{\mathrm{2}} }\:{dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{{a}} \sqrt{\mathrm{1}+\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)}}\:{dx}\:\:\:\:{x}={ua} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{a}}\sqrt{\frac{{a}^{\mathrm{4}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {u}^{\mathrm{2}} }{\mathrm{1}−{u}^{\mathrm{2}} }}\:{du}\:\:\:\:\:\:{cos}\theta={u} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$=\mathrm{4}{a}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}−\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right){cos}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$=\mathrm{4}{a}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}−{e}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}\:{d}\theta=\mathrm{4}{a}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}−{e}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$=\mathrm{4}{aE}\left(\frac{\pi}{\mathrm{2}}\mid{e}\right) \\ $$$${Or}\:\mathrm{4}{a}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}−{e}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:{d}\theta=\mathrm{4}{a}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {e}^{\mathrm{2}{n}} {sin}^{\mathrm{2}{n}} \theta\:{d}\theta \\ $$$$=\mathrm{2}{a}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} {e}^{\mathrm{2}{n}} }{{n}!}.\frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}+\mathrm{1}\right)} \\ $$$$=\mathrm{2}\pi{a}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)_{{n}} }{{n}!\left(\mathrm{1}\right)_{{n}} }{e}^{\mathrm{2}{n}} =\mathrm{2}\pi{a}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}};\mathrm{1};{e}^{\mathrm{2}} \right) \\ $$
Commented by Dwaipayan Shikari last updated on 31/May/21
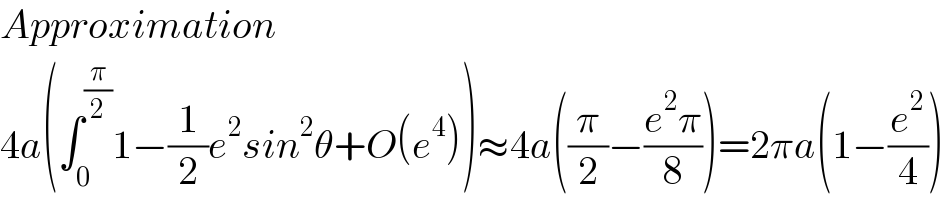
Approximation 4a(∫_0 ^(π/2) 1−(1/2)e^2 sin^2 θ+O(e^4 ))≈4a((π/2)−((e^2 π)/8))=2πa(1−(e^2 /4))
$${Approximation} \\ $$$$\mathrm{4}{a}\left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{e}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{O}\left({e}^{\mathrm{4}} \right)\right)\approx\mathrm{4}{a}\left(\frac{\pi}{\mathrm{2}}−\frac{{e}^{\mathrm{2}} \pi}{\mathrm{8}}\right)=\mathrm{2}\pi{a}\left(\mathrm{1}−\frac{{e}^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$
Answered by ajfour last updated on 01/Jun/21
let A be origin. (((x−a)^2 )/a^2 )+(y^2 /b^2 )=1 (((x−a))/a^2 )+((y((dy/dx)))/b^2 )=0 (dy/dx)=((b^2 (a−x))/(a^2 y)) dl=dx×(√(1+((b^2 (a−x)^2 )/(a^4 {1−(((x−a)^2 )/a^2 )})))) dl=dx(√(1+((b^2 (a−x)^2 )/(a^2 {a^2 −(a−x)^2 })))) =dx(√(1+((b^2 /a^2 )/({(1/((1−(x/a))^2 ))−1})))) let 1−(x/a)=(1/t) , (b/a)=m ⇒ −(dx/a)=−(dt/t^2 ) ⇒ dx=((adt)/t^2 ) dl=((adt)/t^2 )(√(1+(m^2 /(t^2 −1)))) let (m/( (√(t^2 −1))))=tan θ ⇒ t^2 −1=m^2 cot^2 θ tdt=−m^2 cot θcosec^2 θdθ dl=−((am^2 dθ)/(sin^3 θ(1+m^2 cot^2 θ)^(3/2) )) dl=−((am^2 dθ)/((sin^2 θ+m^2 cos^2 θ)^(3/2) )) let sin^2 θ+m^2 cos^2 θ=z^2 (1−m^2 )sin^2 θ=z^2 −m^2 or (1−m^2 )cos^2 θ=1−z^2 ⇒ (1−m^2 )sin θcos θdθ=zdz dθ=((zdz)/( (√(z^2 −m^2 ))(√(1−z^2 )))) dl=−((am^2 dz)/(z^2 (√(z^2 −m^2 ))(√(1−z^2 )))) let z=(√m)s ⇒ dz=(√m)ds dl=((−amds)/(s^2 (√(s^2 −m))(√(1−ms^2 )))) and if (1/s)=v dl=((amv^2 dv)/( (√(1−mv^2 ))(√(v^2 −m)))) dl=((amv^2 dv)/({(1+m^2 )v^2 −m(1+v^4 )}^(1/2) )) 2dl=((a(√m)d(v^2 ))/({(m+(1/m))−(v^2 +(1/v^2 ))}^(1/2) )) say v^2 =X , m+(1/m)=h^2 2dl=((a(√m)dX)/( (√(h^2 −(X+(1/X)))))) .... ........
$${let}\:{A}\:{be}\:{origin}. \\ $$$$\frac{\left({x}−{a}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\frac{\left({x}−{a}\right)}{{a}^{\mathrm{2}} }+\frac{{y}\left(\frac{{dy}}{{dx}}\right)}{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=\frac{{b}^{\mathrm{2}} \left({a}−{x}\right)}{{a}^{\mathrm{2}} {y}} \\ $$$${dl}={dx}×\sqrt{\mathrm{1}+\frac{{b}^{\mathrm{2}} \left({a}−{x}\right)^{\mathrm{2}} }{{a}^{\mathrm{4}} \left\{\mathrm{1}−\frac{\left({x}−{a}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right\}}} \\ $$$$ \\ $$$${dl}={dx}\sqrt{\mathrm{1}+\frac{{b}^{\mathrm{2}} \left({a}−{x}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} \left\{{a}^{\mathrm{2}} −\left({a}−{x}\right)^{\mathrm{2}} \right\}}} \\ $$$$ \\ $$$$\:={dx}\sqrt{\mathrm{1}+\frac{{b}^{\mathrm{2}} /{a}^{\mathrm{2}} }{\left\{\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{{x}}{{a}}\right)^{\mathrm{2}} }−\mathrm{1}\right\}}} \\ $$$${let}\:\:\:\mathrm{1}−\frac{{x}}{{a}}=\frac{\mathrm{1}}{{t}}\:\:,\:\frac{{b}}{{a}}={m} \\ $$$$\Rightarrow\:\:\:−\frac{{dx}}{{a}}=−\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\:{dx}=\frac{{adt}}{{t}^{\mathrm{2}} } \\ $$$${dl}=\frac{{adt}}{{t}^{\mathrm{2}} }\sqrt{\mathrm{1}+\frac{{m}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${let}\:\:\frac{{m}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\:\:\:{t}^{\mathrm{2}} −\mathrm{1}={m}^{\mathrm{2}} \mathrm{cot}\:^{\mathrm{2}} \theta \\ $$$$\:\:\:\:\:{tdt}=−{m}^{\mathrm{2}} \mathrm{cot}\:\theta\mathrm{cosec}\:^{\mathrm{2}} \theta{d}\theta \\ $$$${dl}=−\frac{{am}^{\mathrm{2}} {d}\theta}{\mathrm{sin}\:^{\mathrm{3}} \theta\left(\mathrm{1}+{m}^{\mathrm{2}} \mathrm{cot}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$${dl}=−\frac{{am}^{\mathrm{2}} {d}\theta}{\left(\mathrm{sin}\:^{\mathrm{2}} \theta+{m}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right)^{\mathrm{3}/\mathrm{2}} } \\ $$$${let}\:\:\mathrm{sin}\:^{\mathrm{2}} \theta+{m}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta={z}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{1}−{m}^{\mathrm{2}} \right)\mathrm{sin}\:^{\mathrm{2}} \theta={z}^{\mathrm{2}} −{m}^{\mathrm{2}} \\ $$$${or}\:\:\:\left(\mathrm{1}−{m}^{\mathrm{2}} \right)\mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{1}−{z}^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{m}^{\mathrm{2}} \right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta{d}\theta={zdz} \\ $$$$\:\:\:\:\:{d}\theta=\frac{{zdz}}{\:\sqrt{{z}^{\mathrm{2}} −{m}^{\mathrm{2}} }\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }} \\ $$$${dl}=−\frac{{am}^{\mathrm{2}} {dz}}{{z}^{\mathrm{2}} \sqrt{{z}^{\mathrm{2}} −{m}^{\mathrm{2}} }\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }} \\ $$$${let}\:\:\:{z}=\sqrt{{m}}{s}\:\Rightarrow\:\:{dz}=\sqrt{{m}}{ds} \\ $$$${dl}=\frac{−{amds}}{{s}^{\mathrm{2}} \sqrt{{s}^{\mathrm{2}} −{m}}\sqrt{\mathrm{1}−{ms}^{\mathrm{2}} }} \\ $$$${and}\:{if}\:\:\:\frac{\mathrm{1}}{{s}}={v} \\ $$$${dl}=\frac{{amv}^{\mathrm{2}} {dv}}{\:\sqrt{\mathrm{1}−{mv}^{\mathrm{2}} }\sqrt{{v}^{\mathrm{2}} −{m}}} \\ $$$${dl}=\frac{{amv}^{\mathrm{2}} {dv}}{\left\{\left(\mathrm{1}+{m}^{\mathrm{2}} \right){v}^{\mathrm{2}} −{m}\left(\mathrm{1}+{v}^{\mathrm{4}} \right)\right\}^{\mathrm{1}/\mathrm{2}} } \\ $$$$\mathrm{2}{dl}=\frac{{a}\sqrt{{m}}{d}\left({v}^{\mathrm{2}} \right)}{\left\{\left({m}+\frac{\mathrm{1}}{{m}}\right)−\left({v}^{\mathrm{2}} +\frac{\mathrm{1}}{{v}^{\mathrm{2}} }\right)\right\}^{\mathrm{1}/\mathrm{2}} } \\ $$$${say}\:\:{v}^{\mathrm{2}} ={X}\:,\:{m}+\frac{\mathrm{1}}{{m}}={h}^{\mathrm{2}} \\ $$$$\mathrm{2}{dl}=\frac{{a}\sqrt{{m}}{dX}}{\:\sqrt{{h}^{\mathrm{2}} −\left({X}+\frac{\mathrm{1}}{{X}}\right)}} \\ $$$$…. \\ $$$$…….. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *