Question Number 142461 by bramlexs22 last updated on 01/Jun/21

Commented by qaz last updated on 01/Jun/21
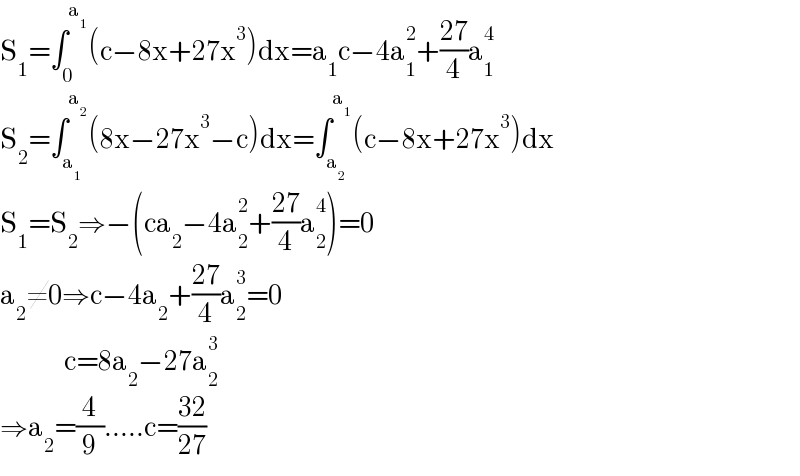
$$\mathrm{S}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{a}_{\mathrm{1}} } \left(\mathrm{c}−\mathrm{8x}+\mathrm{27x}^{\mathrm{3}} \right)\mathrm{dx}=\mathrm{a}_{\mathrm{1}} \mathrm{c}−\mathrm{4a}_{\mathrm{1}} ^{\mathrm{2}} +\frac{\mathrm{27}}{\mathrm{4}}\mathrm{a}_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$\mathrm{S}_{\mathrm{2}} =\int_{\mathrm{a}_{\mathrm{1}} } ^{\mathrm{a}_{\mathrm{2}} } \left(\mathrm{8x}−\mathrm{27x}^{\mathrm{3}} −\mathrm{c}\right)\mathrm{dx}=\int_{\mathrm{a}_{\mathrm{2}} } ^{\mathrm{a}_{\mathrm{1}} } \left(\mathrm{c}−\mathrm{8x}+\mathrm{27x}^{\mathrm{3}} \right)\mathrm{dx} \\ $$$$\mathrm{S}_{\mathrm{1}} =\mathrm{S}_{\mathrm{2}} \Rightarrow−\left(\mathrm{ca}_{\mathrm{2}} −\mathrm{4a}_{\mathrm{2}} ^{\mathrm{2}} +\frac{\mathrm{27}}{\mathrm{4}}\mathrm{a}_{\mathrm{2}} ^{\mathrm{4}} \right)=\mathrm{0} \\ $$$$\mathrm{a}_{\mathrm{2}} \neq\mathrm{0}\Rightarrow\mathrm{c}−\mathrm{4a}_{\mathrm{2}} +\frac{\mathrm{27}}{\mathrm{4}}\mathrm{a}_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{c}=\mathrm{8a}_{\mathrm{2}} −\mathrm{27a}_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{9}}…..\mathrm{c}=\frac{\mathrm{32}}{\mathrm{27}} \\ $$
Answered by benjo_mathlover last updated on 01/Jun/21

Commented by EDWIN88 last updated on 01/Jun/21
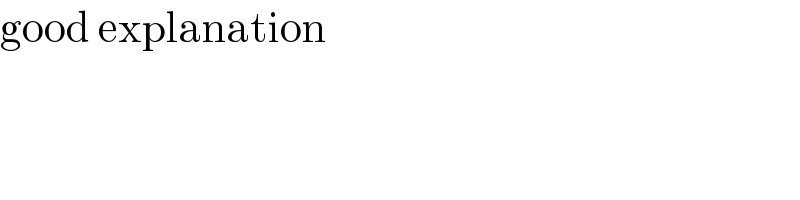
$$\mathrm{good}\:\mathrm{explanation} \\ $$
Answered by mr W last updated on 01/Jun/21
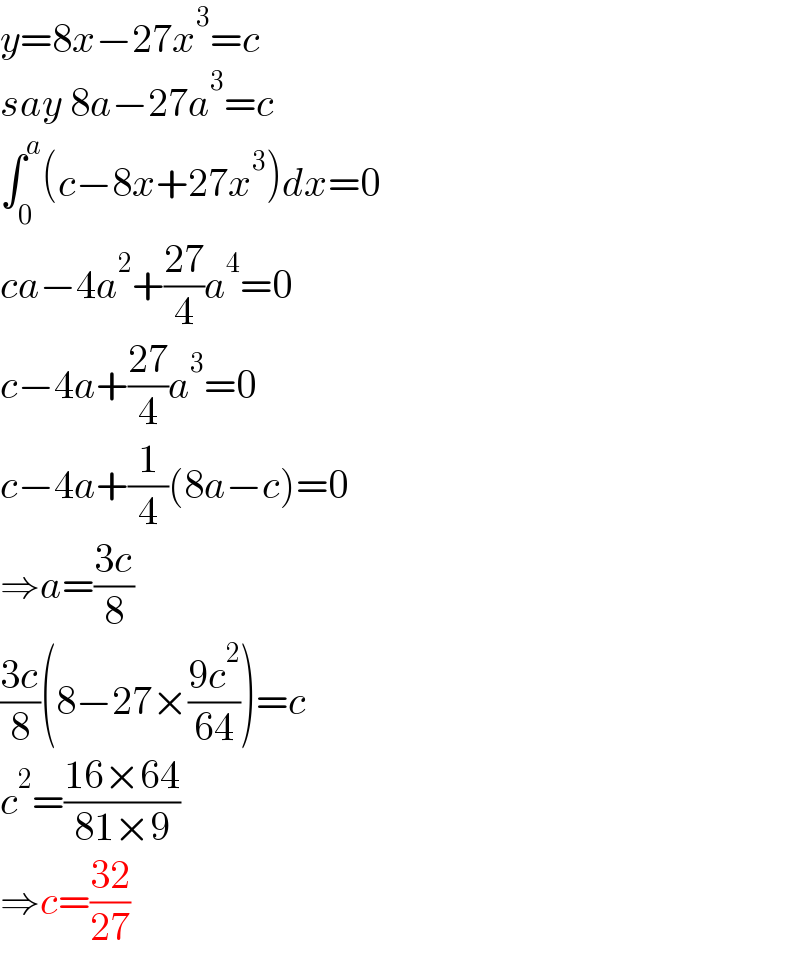
$${y}=\mathrm{8}{x}−\mathrm{27}{x}^{\mathrm{3}} ={c} \\ $$$${say}\:\mathrm{8}{a}−\mathrm{27}{a}^{\mathrm{3}} ={c} \\ $$$$\int_{\mathrm{0}} ^{{a}} \left({c}−\mathrm{8}{x}+\mathrm{27}{x}^{\mathrm{3}} \right){dx}=\mathrm{0} \\ $$$${ca}−\mathrm{4}{a}^{\mathrm{2}} +\frac{\mathrm{27}}{\mathrm{4}}{a}^{\mathrm{4}} =\mathrm{0} \\ $$$${c}−\mathrm{4}{a}+\frac{\mathrm{27}}{\mathrm{4}}{a}^{\mathrm{3}} =\mathrm{0} \\ $$$${c}−\mathrm{4}{a}+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{8}{a}−{c}\right)=\mathrm{0} \\ $$$$\Rightarrow{a}=\frac{\mathrm{3}{c}}{\mathrm{8}} \\ $$$$\frac{\mathrm{3}{c}}{\mathrm{8}}\left(\mathrm{8}−\mathrm{27}×\frac{\mathrm{9}{c}^{\mathrm{2}} }{\mathrm{64}}\right)={c} \\ $$$${c}^{\mathrm{2}} =\frac{\mathrm{16}×\mathrm{64}}{\mathrm{81}×\mathrm{9}} \\ $$$$\Rightarrow{c}=\frac{\mathrm{32}}{\mathrm{27}} \\ $$
Commented by mr W last updated on 01/Jun/21

Commented by mr W last updated on 01/Jun/21
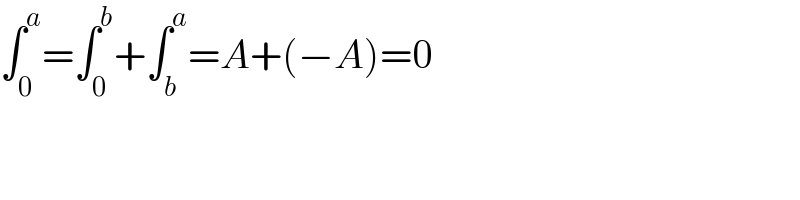
$$\int_{\mathrm{0}} ^{{a}} =\int_{\mathrm{0}} ^{{b}} +\int_{{b}} ^{{a}} ={A}+\left(−{A}\right)=\mathrm{0} \\ $$
Commented by benjo_mathlover last updated on 01/Jun/21

$${oouh}\:\:{great}… \\ $$$$ \\ $$
Commented by benjo_mathlover last updated on 01/Jun/21
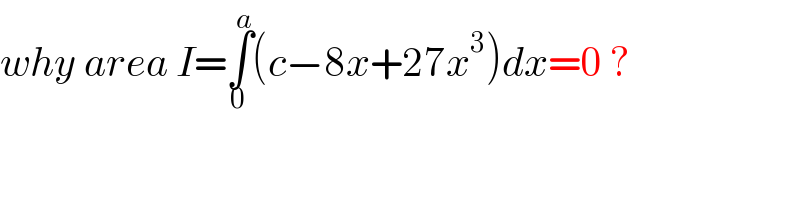
$${why}\:{area}\:{I}=\underset{\mathrm{0}} {\overset{{a}} {\int}}\left({c}−\mathrm{8}{x}+\mathrm{27}{x}^{\mathrm{3}} \right){dx}=\mathrm{0}\:? \\ $$
