Question Number 142462 by BHOOPENDRA last updated on 01/Jun/21

Answered by MJS_new last updated on 01/Jun/21
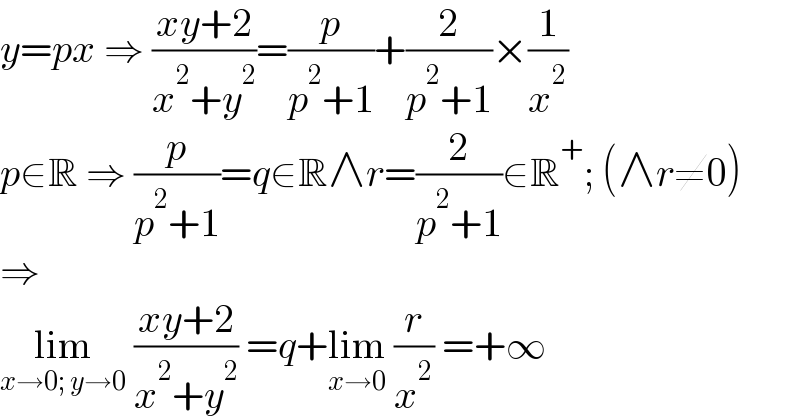
$${y}={px}\:\Rightarrow\:\frac{{xy}+\mathrm{2}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }=\frac{{p}}{{p}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{1}}×\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${p}\in\mathbb{R}\:\Rightarrow\:\frac{{p}}{{p}^{\mathrm{2}} +\mathrm{1}}={q}\in\mathbb{R}\wedge{r}=\frac{\mathrm{2}}{{p}^{\mathrm{2}} +\mathrm{1}}\in\mathbb{R}^{+} ;\:\left(\wedge{r}\neq\mathrm{0}\right) \\ $$$$\Rightarrow \\ $$$$\underset{{x}\rightarrow\mathrm{0};\:{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{xy}+\mathrm{2}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:={q}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{r}}{{x}^{\mathrm{2}} }\:=+\infty \\ $$
Commented by BHOOPENDRA last updated on 01/Jun/21

$${tx}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 01/Jun/21

$$\mathrm{x}=\mathrm{rcos}\theta\:\mathrm{and}\:\mathrm{y}=\mathrm{rsin}\theta\:\Rightarrow\mathrm{lim}_{\left(\mathrm{x},\mathrm{y}\right)\rightarrow\left(\mathrm{0},\mathrm{0}\right)} \frac{\mathrm{xy}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} } \\ $$$$=\mathrm{lim}_{\mathrm{r}\rightarrow\mathrm{0}} \:\:\:\frac{\mathrm{r}^{\mathrm{2}} \mathrm{cos}\theta\:\mathrm{sin}\theta\:+\mathrm{2}}{\mathrm{r}^{\mathrm{2}} }=\mathrm{cos}\theta\mathrm{sin}\theta\:+\mathrm{lim}_{\mathrm{r}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{2}}{\mathrm{r}^{\mathrm{2}} }=+\infty \\ $$
