Menu Close

Question-142499

Tinku Tara 0 Comments
Pin




Question Number 142499 by ajfour last updated on 01/Jun/21
Commented by ajfour last updated on 01/Jun/21
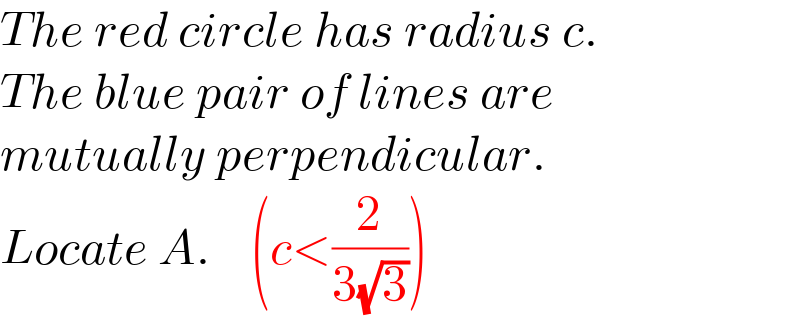
The red circle has radius c. The blue pair of lines are mutually perpendicular. Locate A. (c<(2/(3(√3))))
$${The}\:{red}\:{circle}\:{has}\:{radius}\:{c}. \\ $$$${The}\:{blue}\:{pair}\:{of}\:{lines}\:{are} \\ $$$${mutually}\:{perpendicular}. \\ $$$${Locate}\:{A}.\:\:\:\:\left({c}<\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\right) \\ $$
Answered by mr W last updated on 01/Jun/21
A(p,p^2 ) B(−b,p^2 ) (b/p^2 )=(p^2 /p) ⇒b=p^3 b^2 +(p^2 )^2 =c^2 (p^2 )^3 +(p^2 )^2 =c^2 ((1/p^2 ))^3 −(1/c^2 )((1/p^2 ))−(1/c^2 )=0 ⇒(1/p^2 )=(((1/(2c^2 ))(1+(√(1−(4/(27c^2 )))))))^(1/3) +(((1/(2c^2 ))(1−(√(1−(4/(27c^2 )))))))^(1/3) ⇒p=(1/( (√((((1/(2c^2 ))(1+(√(1−(4/(27c^2 )))))))^(1/3) +(((1/(2c^2 ))(1−(√(1−(4/(27c^2 )))))))^(1/3) ))))
$${A}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${B}\left(−{b},{p}^{\mathrm{2}} \right) \\ $$$$\frac{{b}}{{p}^{\mathrm{2}} }=\frac{{p}^{\mathrm{2}} }{{p}} \\ $$$$\Rightarrow{b}={p}^{\mathrm{3}} \\ $$$${b}^{\mathrm{2}} +\left({p}^{\mathrm{2}} \right)^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\left({p}^{\mathrm{2}} \right)^{\mathrm{3}} +\left({p}^{\mathrm{2}} \right)^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\right)^{\mathrm{3}} −\frac{\mathrm{1}}{{c}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\right)−\frac{\mathrm{1}}{{c}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{p}^{\mathrm{2}} }=\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} }\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{27}{c}^{\mathrm{2}} }}\right)}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} }\left(\mathrm{1}−\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{27}{c}^{\mathrm{2}} }}\right)} \\ $$$$\Rightarrow{p}=\frac{\mathrm{1}}{\:\sqrt{\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} }\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{27}{c}^{\mathrm{2}} }}\right)}+\sqrt[{\mathrm{3}}]{\frac{\mathrm{1}}{\mathrm{2}{c}^{\mathrm{2}} }\left(\mathrm{1}−\sqrt{\mathrm{1}−\frac{\mathrm{4}}{\mathrm{27}{c}^{\mathrm{2}} }}\right)}}} \\ $$
Commented by mr W last updated on 01/Jun/21
Commented by mr W last updated on 01/Jun/21
Commented by ajfour last updated on 01/Jun/21
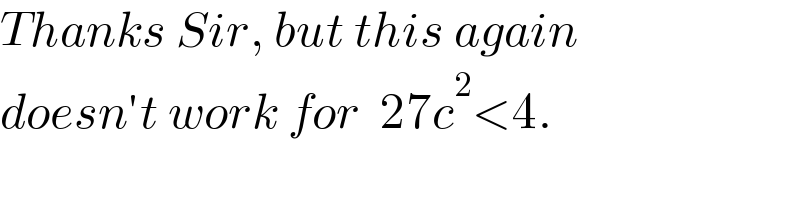
Thanks Sir, but this again doesn′t work for 27c^2 <4.
$${Thanks}\:{Sir},\:{but}\:{this}\:{again} \\ $$$${doesn}'{t}\:{work}\:{for}\:\:\mathrm{27}{c}^{\mathrm{2}} <\mathrm{4}. \\ $$
Commented by mr W last updated on 01/Jun/21
yes.
$${yes}. \\ $$
Answered by ajfour last updated on 01/Jun/21
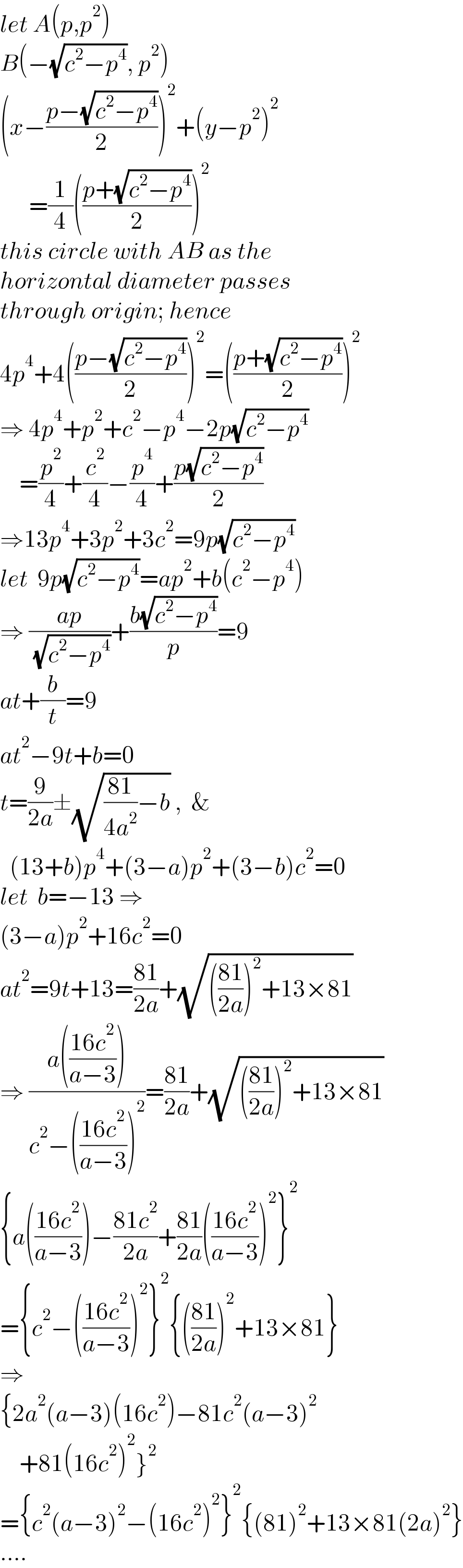
let A(p,p^2 ) B(−(√(c^2 −p^4 )), p^2 ) (x−((p−(√(c^2 −p^4 )))/2))^2 +(y−p^2 )^2 =(1/4)(((p+(√(c^2 −p^4 )))/2))^2 this circle with AB as the horizontal diameter passes through origin; hence 4p^4 +4(((p−(√(c^2 −p^4 )))/2))^2 =(((p+(√(c^2 −p^4 )))/2))^2 ⇒ 4p^4 +p^2 +c^2 −p^4 −2p(√(c^2 −p^4 )) =(p^2 /4)+(c^2 /4)−(p^4 /4)+((p(√(c^2 −p^4 )))/2) ⇒13p^4 +3p^2 +3c^2 =9p(√(c^2 −p^4 )) let 9p(√(c^2 −p^4 ))=ap^2 +b(c^2 −p^4 ) ⇒ ((ap)/( (√(c^2 −p^4 ))))+((b(√(c^2 −p^4 )))/p)=9 at+(b/t)=9 at^2 −9t+b=0 t=(9/(2a))±(√(((81)/(4a^2 ))−b)) , & (13+b)p^4 +(3−a)p^2 +(3−b)c^2 =0 let b=−13 ⇒ (3−a)p^2 +16c^2 =0 at^2 =9t+13=((81)/(2a))+(√((((81)/(2a)))^2 +13×81)) ⇒ ((a(((16c^2 )/(a−3))))/(c^2 −(((16c^2 )/(a−3)))^2 ))=((81)/(2a))+(√((((81)/(2a)))^2 +13×81)) {a(((16c^2 )/(a−3)))−((81c^2 )/(2a))+((81)/(2a))(((16c^2 )/(a−3)))^2 }^2 ={c^2 −(((16c^2 )/(a−3)))^2 }^2 {(((81)/(2a)))^2 +13×81} ⇒ {2a^2 (a−3)(16c^2 )−81c^2 (a−3)^2 +81(16c^2 )^2 }^2 ={c^2 (a−3)^2 −(16c^2 )^2 }^2 {(81)^2 +13×81(2a)^2 } ....
$${let}\:{A}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${B}\left(−\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} },\:{p}^{\mathrm{2}} \right) \\ $$$$\left({x}−\frac{{p}−\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}−{p}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{p}+\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${this}\:{circle}\:{with}\:{AB}\:{as}\:{the} \\ $$$${horizontal}\:{diameter}\:{passes} \\ $$$${through}\:{origin};\:{hence} \\ $$$$\mathrm{4}{p}^{\mathrm{4}} +\mathrm{4}\left(\frac{{p}−\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{{p}+\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{4}{p}^{\mathrm{4}} +{p}^{\mathrm{2}} +{c}^{\mathrm{2}} −{p}^{\mathrm{4}} −\mathrm{2}{p}\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} } \\ $$$$\:\:\:\:=\frac{{p}^{\mathrm{2}} }{\mathrm{4}}+\frac{{c}^{\mathrm{2}} }{\mathrm{4}}−\frac{{p}^{\mathrm{4}} }{\mathrm{4}}+\frac{{p}\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{13}{p}^{\mathrm{4}} +\mathrm{3}{p}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} =\mathrm{9}{p}\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} } \\ $$$${let}\:\:\mathrm{9}{p}\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }={ap}^{\mathrm{2}} +{b}\left({c}^{\mathrm{2}} −{p}^{\mathrm{4}} \right) \\ $$$$\Rightarrow\:\frac{{ap}}{\:\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}+\frac{{b}\sqrt{{c}^{\mathrm{2}} −{p}^{\mathrm{4}} }}{{p}}=\mathrm{9} \\ $$$${at}+\frac{{b}}{{t}}=\mathrm{9} \\ $$$${at}^{\mathrm{2}} −\mathrm{9}{t}+{b}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{9}}{\mathrm{2}{a}}\pm\sqrt{\frac{\mathrm{81}}{\mathrm{4}{a}^{\mathrm{2}} }−{b}}\:,\:\:\& \\ $$$$\:\:\left(\mathrm{13}+{b}\right){p}^{\mathrm{4}} +\left(\mathrm{3}−{a}\right){p}^{\mathrm{2}} +\left(\mathrm{3}−{b}\right){c}^{\mathrm{2}} =\mathrm{0} \\ $$$${let}\:\:{b}=−\mathrm{13}\:\Rightarrow \\ $$$$\left(\mathrm{3}−{a}\right){p}^{\mathrm{2}} +\mathrm{16}{c}^{\mathrm{2}} =\mathrm{0} \\ $$$${at}^{\mathrm{2}} =\mathrm{9}{t}+\mathrm{13}=\frac{\mathrm{81}}{\mathrm{2}{a}}+\sqrt{\left(\frac{\mathrm{81}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\mathrm{13}×\mathrm{81}} \\ $$$$\Rightarrow\:\frac{{a}\left(\frac{\mathrm{16}{c}^{\mathrm{2}} }{{a}−\mathrm{3}}\right)}{{c}^{\mathrm{2}} −\left(\frac{\mathrm{16}{c}^{\mathrm{2}} }{{a}−\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{81}}{\mathrm{2}{a}}+\sqrt{\left(\frac{\mathrm{81}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\mathrm{13}×\mathrm{81}} \\ $$$$\left\{{a}\left(\frac{\mathrm{16}{c}^{\mathrm{2}} }{{a}−\mathrm{3}}\right)−\frac{\mathrm{81}{c}^{\mathrm{2}} }{\mathrm{2}{a}}+\frac{\mathrm{81}}{\mathrm{2}{a}}\left(\frac{\mathrm{16}{c}^{\mathrm{2}} }{{a}−\mathrm{3}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$=\left\{{c}^{\mathrm{2}} −\left(\frac{\mathrm{16}{c}^{\mathrm{2}} }{{a}−\mathrm{3}}\right)^{\mathrm{2}} \right\}^{\mathrm{2}} \left\{\left(\frac{\mathrm{81}}{\mathrm{2}{a}}\right)^{\mathrm{2}} +\mathrm{13}×\mathrm{81}\right\} \\ $$$$\Rightarrow \\ $$$$\left\{\mathrm{2}{a}^{\mathrm{2}} \left({a}−\mathrm{3}\right)\left(\mathrm{16}{c}^{\mathrm{2}} \right)−\mathrm{81}{c}^{\mathrm{2}} \left({a}−\mathrm{3}\right)^{\mathrm{2}} \right. \\ $$$$\left.\:\:\:\:+\mathrm{81}\left(\mathrm{16}{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}^{\mathrm{2}} \\ $$$$=\left\{{c}^{\mathrm{2}} \left({a}−\mathrm{3}\right)^{\mathrm{2}} −\left(\mathrm{16}{c}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}^{\mathrm{2}} \left\{\left(\mathrm{81}\right)^{\mathrm{2}} +\mathrm{13}×\mathrm{81}\left(\mathrm{2}{a}\right)^{\mathrm{2}} \right\} \\ $$$$…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *