Question Number 142503 by Gbenga last updated on 01/Jun/21

Answered by mr W last updated on 01/Jun/21
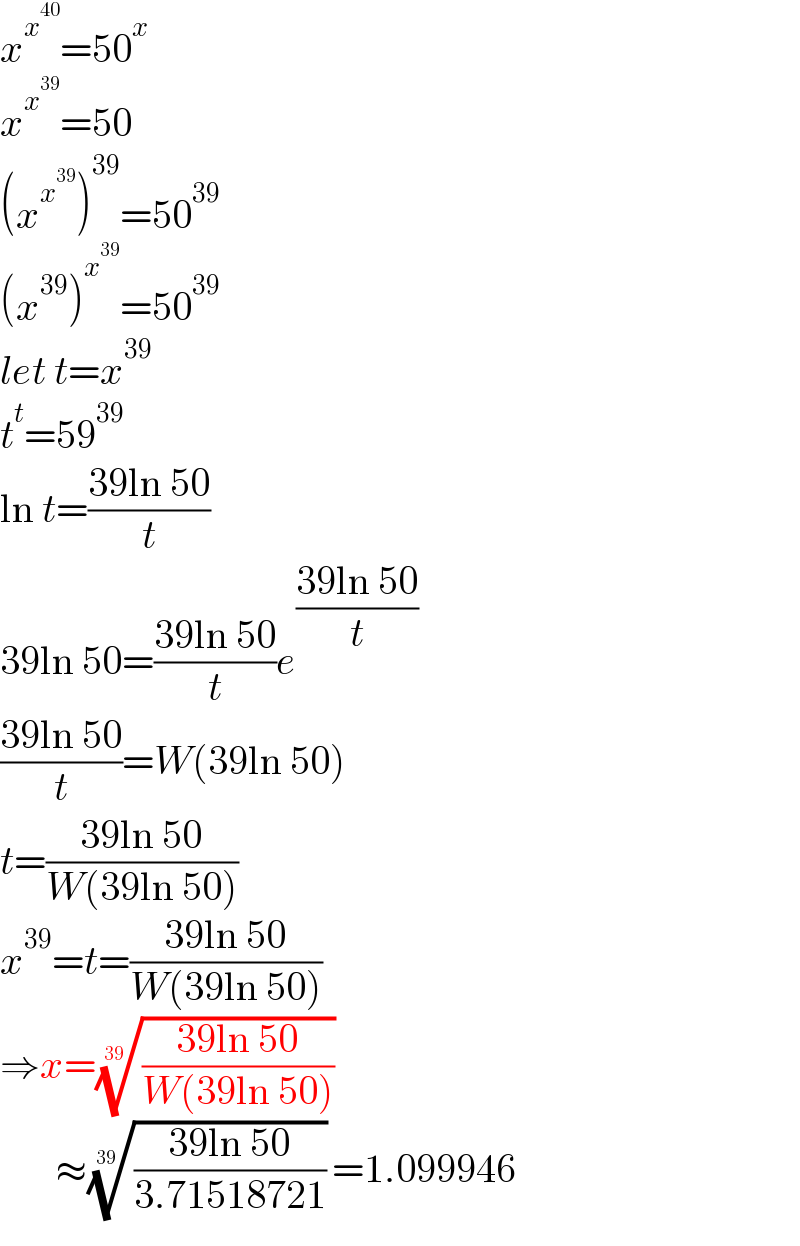
$${x}^{{x}^{\mathrm{40}} } =\mathrm{50}^{{x}} \\ $$$${x}^{{x}^{\mathrm{39}} } =\mathrm{50} \\ $$$$\left({x}^{{x}^{\mathrm{39}} } \right)^{\mathrm{39}} =\mathrm{50}^{\mathrm{39}} \\ $$$$\left({x}^{\mathrm{39}} \right)^{{x}^{\mathrm{39}} } =\mathrm{50}^{\mathrm{39}} \\ $$$${let}\:{t}={x}^{\mathrm{39}} \\ $$$${t}^{{t}} =\mathrm{59}^{\mathrm{39}} \\ $$$$\mathrm{ln}\:{t}=\frac{\mathrm{39ln}\:\mathrm{50}}{{t}} \\ $$$$\mathrm{39ln}\:\mathrm{50}=\frac{\mathrm{39ln}\:\mathrm{50}}{{t}}{e}^{\frac{\mathrm{39ln}\:\mathrm{50}}{{t}}} \\ $$$$\frac{\mathrm{39ln}\:\mathrm{50}}{{t}}={W}\left(\mathrm{39ln}\:\mathrm{50}\right) \\ $$$${t}=\frac{\mathrm{39ln}\:\mathrm{50}}{{W}\left(\mathrm{39ln}\:\mathrm{50}\right)} \\ $$$${x}^{\mathrm{39}} ={t}=\frac{\mathrm{39ln}\:\mathrm{50}}{{W}\left(\mathrm{39ln}\:\mathrm{50}\right)} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{39}}]{\frac{\mathrm{39ln}\:\mathrm{50}}{{W}\left(\mathrm{39ln}\:\mathrm{50}\right)}} \\ $$$$\:\:\:\:\:\:\:\approx\sqrt[{\mathrm{39}}]{\frac{\mathrm{39ln}\:\mathrm{50}}{\mathrm{3}.\mathrm{71518721}}}=\mathrm{1}.\mathrm{099946} \\ $$
