Question Number 142603 by mohammad17 last updated on 02/Jun/21
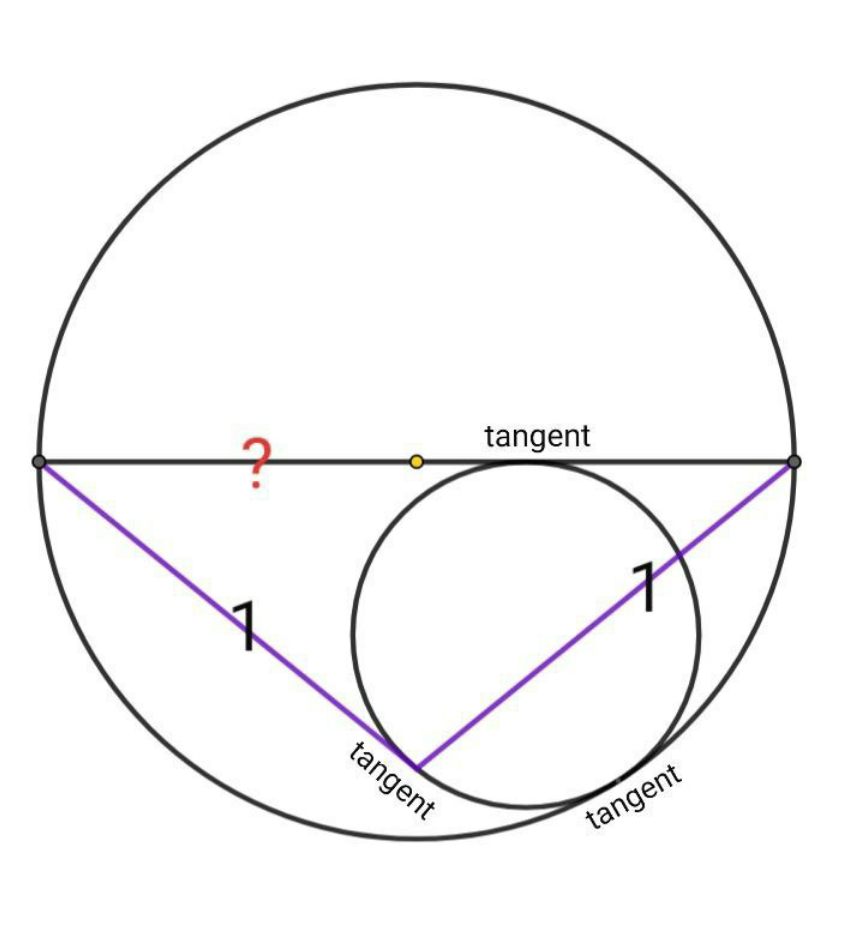
Answered by mr W last updated on 03/Jun/21
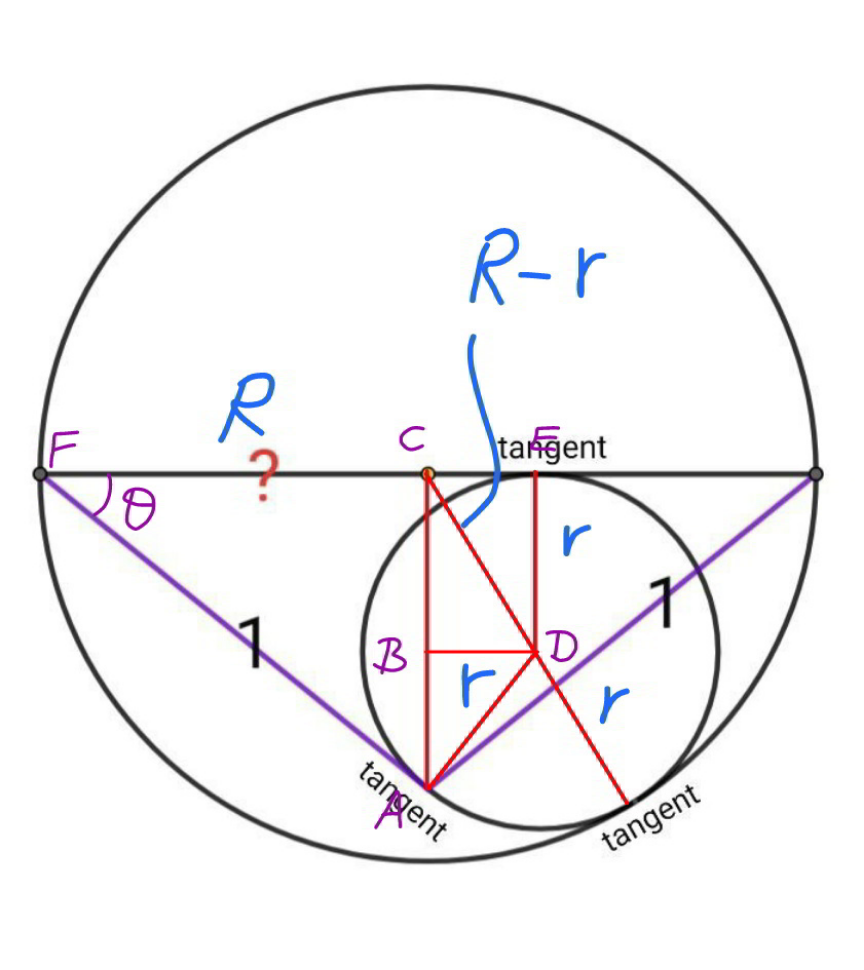
Commented by mr W last updated on 03/Jun/21
![CE=(√((R−r)^2 −r^2 ))=(√(R^2 −2Rr)) FE=R+(√(R^2 −2Rr))=FA=1 ⇒R^2 −2Rr=(1−R)^2 ⇒R^2 −2Rr=1−2R+R^2 ⇒2R(1−r)=1 ⇒r=1−(1/(2R)) cos θ=(R/1)=R tan (θ/2)=(r/1)=r ⇒R=((1−r^2 )/(1+r^2 ))=(2/(1+r^2 ))−1 ⇒(R+1)(1+r^2 )=2 ⇒(R+1)[1+(1−(1/(2R)))^2 ]=2 ⇒(R+1)[4R^2 +(2R−1)^2 ]=8R^2 ⇒8R^3 −4R^2 −3R+1=0 ⇒R≈0.7757](https://www.tinkutara.com/question/Q142610.png)
$${CE}=\sqrt{\left({R}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}} \\ $$$${FE}={R}+\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}}={FA}=\mathrm{1} \\ $$$$\Rightarrow{R}^{\mathrm{2}} −\mathrm{2}{Rr}=\left(\mathrm{1}−{R}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}^{\mathrm{2}} −\mathrm{2}{Rr}=\mathrm{1}−\mathrm{2}{R}+{R}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{R}\left(\mathrm{1}−{r}\right)=\mathrm{1} \\ $$$$\Rightarrow{r}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$$ \\ $$$$\mathrm{cos}\:\theta=\frac{{R}}{\mathrm{1}}={R} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{r}}{\mathrm{1}}={r} \\ $$$$\Rightarrow{R}=\frac{\mathrm{1}−{r}^{\mathrm{2}} }{\mathrm{1}+{r}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{1}+{r}^{\mathrm{2}} }−\mathrm{1} \\ $$$$\Rightarrow\left({R}+\mathrm{1}\right)\left(\mathrm{1}+{r}^{\mathrm{2}} \right)=\mathrm{2} \\ $$$$\Rightarrow\left({R}+\mathrm{1}\right)\left[\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{R}}\right)^{\mathrm{2}} \right]=\mathrm{2} \\ $$$$\Rightarrow\left({R}+\mathrm{1}\right)\left[\mathrm{4}{R}^{\mathrm{2}} +\left(\mathrm{2}{R}−\mathrm{1}\right)^{\mathrm{2}} \right]=\mathrm{8}{R}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{8}{R}^{\mathrm{3}} −\mathrm{4}{R}^{\mathrm{2}} −\mathrm{3}{R}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{R}\approx\mathrm{0}.\mathrm{7757} \\ $$
