Question-142725

Question Number 142725 by mathlove last updated on 04/Jun/21

Commented by Olaf_Thorendsen last updated on 04/Jun/21

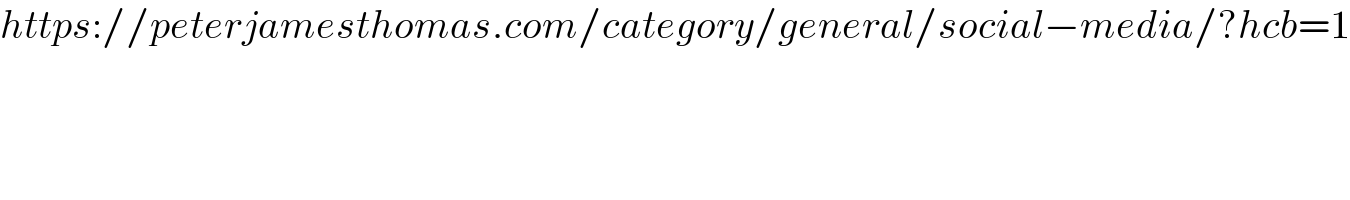
https://peterjamesthomas.com/category/general/social−media/?hcb=1

$${https}://{peterjamesthomas}.{com}/{category}/{general}/{social}−{media}/?{hcb}=\mathrm{1} \\ $$

Commented by MJS_new last updated on 04/Jun/21

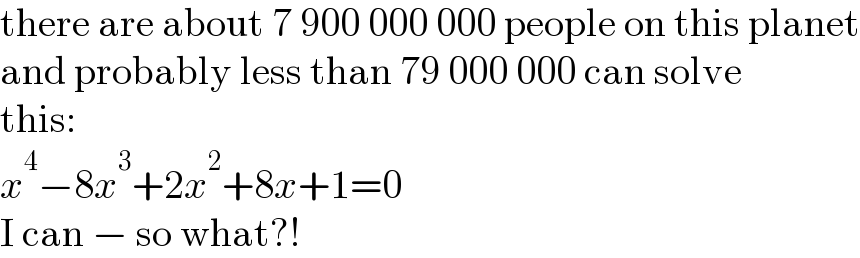
there are about 7 900 000 000 people on this planet and probably less than 79 000 000 can solve this: x^4 −8x^3 +2x^2 +8x+1=0 I can − so what?!

$$\mathrm{there}\:\mathrm{are}\:\mathrm{about}\:\mathrm{7}\:\mathrm{900}\:\mathrm{000}\:\mathrm{000}\:\mathrm{people}\:\mathrm{on}\:\mathrm{this}\:\mathrm{planet} \\ $$$$\mathrm{and}\:\mathrm{probably}\:\mathrm{less}\:\mathrm{than}\:\mathrm{79}\:\mathrm{000}\:\mathrm{000}\:\mathrm{can}\:\mathrm{solve} \\ $$$$\mathrm{this}: \\ $$$${x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{can}\:−\:\mathrm{so}\:\mathrm{what}?! \\ $$

Commented by 1549442205PVT last updated on 05/Jun/21

This equation is too easy! x^4 −8x^3 +2x^2 +8x+1=0 ⇔(x^2 +(1/x^2 ))−8(x−(1/x))+2=0.put (x−(1/x))=t we get t^2 +2−8t+2=0⇔t^2 −8t+4=0 Δ′=12=(2(√3))^2 ⇒t=4±2(√3) i)x−(1/x)=4+2(√3) ⇔x^2 −(4+2(√3))x−1=0 Δ′=(2+(√3))^2 +1=8+4(√3)=[(√2)((√3)+1)]^2 x=2+(√3)±((√6)+(√2)) ii)x−(1/x)=4−2(√3)⇔x^2 −2(2−(√3))x−1=0 Δ′=(2−(√3))^2 +1=8−4(√3)=((√6)−(√2))^2 x=2−(√3)±((√6)−(√2))

$$\mathrm{This}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{too}\:\mathrm{easy}! \\ $$$$\mathrm{x}^{\mathrm{4}} −\mathrm{8x}^{\mathrm{3}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{8x}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)−\mathrm{8}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{2}=\mathrm{0}.\mathrm{put}\:\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{t} \\ $$$$\mathrm{we}\:\mathrm{get}\:\:\mathrm{t}^{\mathrm{2}} +\mathrm{2}−\mathrm{8t}+\mathrm{2}=\mathrm{0}\Leftrightarrow\mathrm{t}^{\mathrm{2}} −\mathrm{8t}+\mathrm{4}=\mathrm{0} \\ $$$$\Delta'=\mathrm{12}=\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \Rightarrow\mathrm{t}=\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\left.\mathrm{i}\right)\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\:\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta'=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{8}+\mathrm{4}\sqrt{\mathrm{3}}=\left[\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\right]^{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{2}+\sqrt{\mathrm{3}}\pm\left(\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\right) \\ $$$$\left.\mathrm{ii}\right)\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Delta'=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}=\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{2}−\sqrt{\mathrm{3}}\pm\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right) \\ $$

Commented by MJS_new last updated on 05/Jun/21

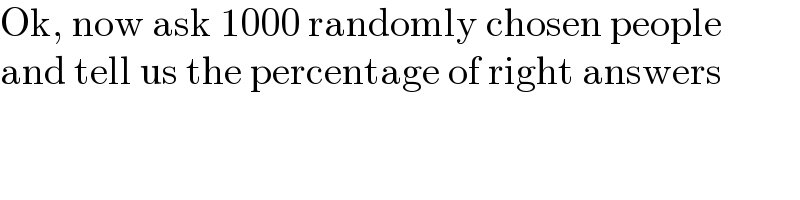
Ok, now ask 1000 randomly chosen people and tell us the percentage of right answers

$$\mathrm{Ok},\:\mathrm{now}\:\mathrm{ask}\:\mathrm{1000}\:\mathrm{randomly}\:\mathrm{chosen}\:\mathrm{people} \\ $$$$\mathrm{and}\:\mathrm{tell}\:\mathrm{us}\:\mathrm{the}\:\mathrm{percentage}\:\mathrm{of}\:\mathrm{right}\:\mathrm{answers} \\ $$

Commented by Dwaipayan Shikari last updated on 05/Jun/21

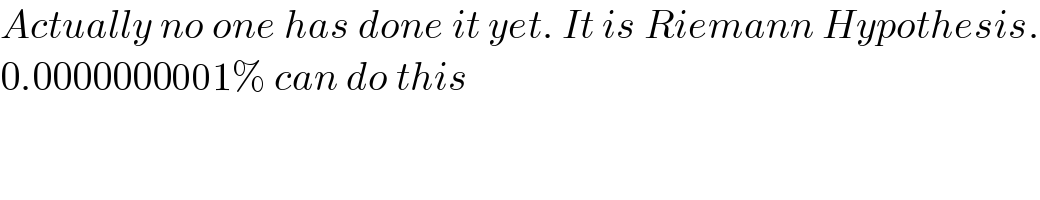
Actually no one has done it yet. It is Riemann Hypothesis. 0.0000000001% can do this

$${Actually}\:{no}\:{one}\:{has}\:{done}\:{it}\:{yet}.\:{It}\:{is}\:{Riemann}\:{Hypothesis}. \\ $$$$\mathrm{0}.\mathrm{0000000001\%}\:{can}\:{do}\:{this} \\ $$

Commented by MJS_new last updated on 05/Jun/21

I know. but follow the link posted by Sir Olaf.

$$\mathrm{I}\:\mathrm{know}.\:\mathrm{but}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{link}\:\mathrm{posted}\:\mathrm{by}\:\mathrm{Sir}\:\mathrm{Olaf}. \\ $$

Commented by Tawa11 last updated on 06/Nov/21

$$\mathrm{Nice} \\ $$

Answered by Dwaipayan Shikari last updated on 05/Jun/21

z=w+bi Σ_(n=1) ^∞ (1/n^z )=Σ_(n=1) ^∞ n^(−w) n^(−bi) =Σ_(n=1) ^∞ n^(−w) e^(−bilog(n)) =Σ_(n=1) ^∞ n^(−w) cos(blog(n))−in^(−w) sin(blog(n)) ℜ(ζ(z))=Σ_(n=1) ^∞ ((cos(blog(n)))/n^w ) Now Σ_(n=1) ^∞ ((cos(blog(n)))/n^w )−i((sin(blog(n))/n^w ) =0 People believe that ℜ(z)=(1/2)

$${z}={w}+{bi} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{z}} }=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−{w}} {n}^{−{bi}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−{w}} {e}^{−{bilog}\left({n}\right)} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−{w}} {cos}\left({blog}\left({n}\right)\right)−{in}^{−{w}} {sin}\left({blog}\left({n}\right)\right) \\ $$$$\Re\left(\zeta\left({z}\right)\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left({blog}\left({n}\right)\right)}{{n}^{{w}} } \\ $$$${Now}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left({blog}\left({n}\right)\right)}{{n}^{{w}} }−{i}\frac{{sin}\left({blog}\left({n}\right)\right.}{{n}^{{w}} }\:=\mathrm{0} \\ $$$${People}\:{believe}\:{that}\:\Re\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by MJS_new last updated on 04/Jun/21

$$\mathrm{welcome}\:\mathrm{among}\:\mathrm{the}\:\mathrm{chosen}\:\mathrm{few}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply