Menu Close

Question-142763

Tinku Tara 0 Comments
Pin




Question Number 142763 by lapache last updated on 05/Jun/21
Commented by Ar Brandon last updated on 05/Jun/21
I=∫(√(tanx))dx , t^2 =tanx ⇒2tdt=(1+t^4 )dx =∫((2t^2 dt)/(1+t^4 ))=∫(((t^2 +1)+(t^2 −1))/(t^4 +1))dt =∫((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt+∫((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt=∫((1+(1/t^2 ))/((t−(1/t))^2 +2))dt+∫((1−(1/t^2 ))/((t+(1/t))^2 −2))dt =∫(du/(u^2 +2))+∫(dv/(v^2 −2))=((arctan(u/(√2)))/( (√2)))−((arctanh(v/(√2)))/( (√2)))+C =(1/( (√2)))arctan(((t^2 −1)/( (√2)t)))−(1/(2(√2)))ln∣((t^2 +(√2)t+1)/(t^2 −(√2)t+1))∣+C =(1/( (√2)))arctan(((tanx−1)/( (√(2tanx)))))−(1/(2(√2)))ln∣((tanx+(√(2tanx))+1)/(tanx−(√(2tanx))+1))∣+C
$$\mathcal{I}=\int\sqrt{\mathrm{tanx}}\mathrm{dx}\:,\:\mathrm{t}^{\mathrm{2}} =\mathrm{tanx}\:\Rightarrow\mathrm{2tdt}=\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)\mathrm{dx} \\ $$$$\:\:\:=\int\frac{\mathrm{2t}^{\mathrm{2}} \mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }=\int\frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:=\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}+\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}=\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt}+\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt} \\ $$$$\:\:\:=\int\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}+\int\frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}=\frac{\mathrm{arctan}\left(\mathrm{u}/\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{arctanh}\left(\mathrm{v}/\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}+\mathrm{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{2}}\mathrm{t}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}\mathrm{t}+\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}\mathrm{t}+\mathrm{1}}\mid+\mathrm{C} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{tanx}−\mathrm{1}}{\:\sqrt{\mathrm{2tanx}}}\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{tanx}+\sqrt{\mathrm{2tanx}}+\mathrm{1}}{\mathrm{tanx}−\sqrt{\mathrm{2tanx}}+\mathrm{1}}\mid+\mathrm{C} \\ $$
Commented by Tinku Tara last updated on 05/Jun/21
Please updste to latest version. Watermark has been removed in latest version (free)
$$\mathrm{Please}\:\mathrm{updste}\:\mathrm{to}\:\mathrm{latest}\:\mathrm{version}. \\ $$$$\mathrm{Watermark}\:\mathrm{has}\:\mathrm{been}\:\mathrm{removed}\:\mathrm{in} \\ $$$$\mathrm{latest}\:\mathrm{version}\:\left(\mathrm{free}\right) \\ $$
Answered by Ar Brandon last updated on 05/Jun/21
I=∫_0 ^(π/2) (√(tanx))dx , t^2 =tanx ⇒2tdt=(1+t^4 )dx =∫_0 ^∞ ((2t^2 dt)/(1+t^4 ))=∫_0 ^∞ (((t^2 +1)+(t^2 −1))/(t^4 +1))dt =∫_0 ^∞ ((1+(1/t^2 ))/(t^2 +(1/t^2 )))dt+∫_0 ^∞ ((1−(1/t^2 ))/(t^2 +(1/t^2 )))dt=∫_0 ^∞ ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt+∫_0 ^∞ ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt =∫_(−∞) ^∞ (du/(u^2 +2))+∫_(+∞) ^(+∞) (dv/(v^2 −2))=[((arctan(u/(√2)))/( (√2)))]_(−∞) ^(+∞) =(1/( (√2)))((π/2)+(π/2))=(π/( (√2)))
$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{tanx}}\mathrm{dx}\:,\:\mathrm{t}^{\mathrm{2}} =\mathrm{tanx}\:\Rightarrow\mathrm{2tdt}=\left(\mathrm{1}+\mathrm{t}^{\mathrm{4}} \right)\mathrm{dx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2t}^{\mathrm{2}} \mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }=\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt} \\ $$$$\:\:\:=\int_{−\infty} ^{\infty} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}+\int_{+\infty} ^{+\infty} \frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}=\left[\frac{\mathrm{arctan}\left(\mathrm{u}/\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}\right]_{−\infty} ^{+\infty} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by mathmax by abdo last updated on 06/Jun/21
Φ= ∫_0 ^(π/2) (√(tanx))dx changement (√(tanx))=t give tanx =t^2 ⇒x=arctan(t^2 ) ⇒ Φ=∫_0 ^∞ ((t.(2t))/(1+t^4 ))dt =∫_(−∞) ^(+∞) (t^2 /(1+t^4 ))dt let ϕ(z)=(z^2 /(z^4 +1)) ⇒ϕ(z)=(z^2 /((z^2 −i)(z^2 +i))) =(z^2 /((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{Res(ϕ,e^((iπ)/4) ) +Res(ϕ,−e^(−((iπ)/4)) )} we have Res(ϕ,e^((iπ)/4) )=(i/(2e^((iπ)/4) (2i))) =(1/4)e^(−((iπ)/4)) Res(ϕ,−e^(−((iπ)/4)) )=((−i)/((−2e^(−((iπ)/4)) )(−2i))) =−(1/4)e^((iπ)/4) ⇒ ∫_R ϕ(z)dz =−2iπ{(1/4)e^((iπ)/4) −(1/4)e^(−((iπ)/4)) } =−((πi)/2)(2isin((π/4))) =π.(1/( (√2)))=(π/( (√2))) ⇒Φ=(π/( (√2)))
$$\Phi=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{tanx}}\mathrm{dx}\:\mathrm{changement}\:\sqrt{\mathrm{tanx}}=\mathrm{t}\:\mathrm{give}\:\mathrm{tanx}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}=\mathrm{arctan}\left(\mathrm{t}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\Phi=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}.\left(\mathrm{2t}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{z}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$$\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{i}\right)}\:=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{z}+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \\ $$$$\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\:+\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)=\frac{\mathrm{i}}{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \left(\mathrm{2i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)=\frac{−\mathrm{i}}{\left(−\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)\left(−\mathrm{2i}\right)}\:=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=−\mathrm{2i}\pi\left\{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4}}} −\frac{\mathrm{1}}{\mathrm{4}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right\} \\ $$$$=−\frac{\pi\mathrm{i}}{\mathrm{2}}\left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{4}}\right)\right)\:=\pi.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\Phi=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Answered by Ar Brandon last updated on 05/Jun/21
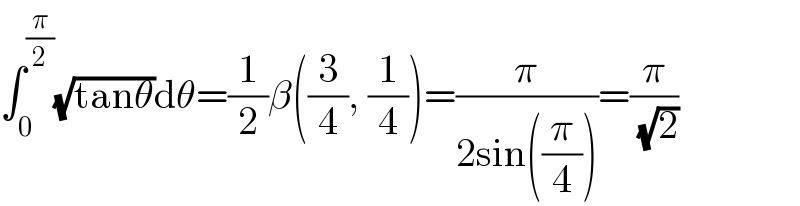
∫_0 ^(π/2) (√(tanθ))dθ=(1/2)β((3/4), (1/4))=(π/(2sin((π/4))))=(π/( (√2)))
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{tan}\theta}\mathrm{d}\theta=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{3}}{\mathrm{4}},\:\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\pi}{\mathrm{2sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *