Question-142788

Question Number 142788 by mohammad17 last updated on 05/Jun/21

Answered by qaz last updated on 05/Jun/21

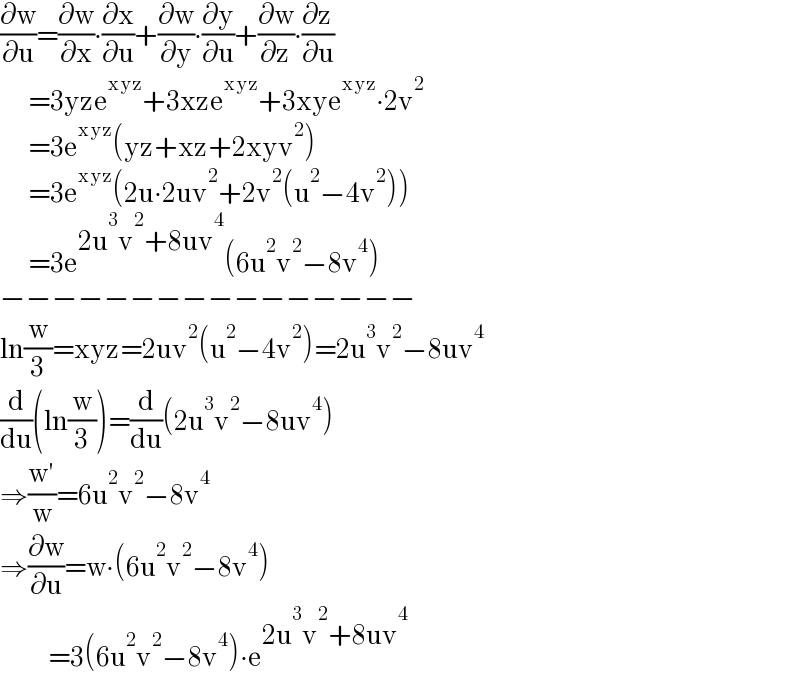
(∂w/∂u)=(∂w/∂x)∙(∂x/∂u)+(∂w/∂y)∙(∂y/∂u)+(∂w/∂z)∙(∂z/∂u) =3yze^(xyz) +3xze^(xyz) +3xye^(xyz) ∙2v^2 =3e^(xyz) (yz+xz+2xyv^2 ) =3e^(xyz) (2u∙2uv^2 +2v^2 (u^2 −4v^2 )) =3e^(2u^3 v^2 +8uv^4 ) (6u^2 v^2 −8v^4 ) −−−−−−−−−−−−−−−− ln(w/3)=xyz=2uv^2 (u^2 −4v^2 )=2u^3 v^2 −8uv^4 (d/du)(ln(w/3))=(d/du)(2u^3 v^2 −8uv^4 ) ⇒((w′)/w)=6u^2 v^2 −8v^4 ⇒(∂w/∂u)=w∙(6u^2 v^2 −8v^4 ) =3(6u^2 v^2 −8v^4 )∙e^(2u^3 v^2 +8uv^4 )

$$\frac{\partial\mathrm{w}}{\partial\mathrm{u}}=\frac{\partial\mathrm{w}}{\partial\mathrm{x}}\centerdot\frac{\partial\mathrm{x}}{\partial\mathrm{u}}+\frac{\partial\mathrm{w}}{\partial\mathrm{y}}\centerdot\frac{\partial\mathrm{y}}{\partial\mathrm{u}}+\frac{\partial\mathrm{w}}{\partial\mathrm{z}}\centerdot\frac{\partial\mathrm{z}}{\partial\mathrm{u}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{3yze}^{\mathrm{xyz}} +\mathrm{3xze}^{\mathrm{xyz}} +\mathrm{3xye}^{\mathrm{xyz}} \centerdot\mathrm{2v}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{3e}^{\mathrm{xyz}} \left(\mathrm{yz}+\mathrm{xz}+\mathrm{2xyv}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{3e}^{\mathrm{xyz}} \left(\mathrm{2u}\centerdot\mathrm{2uv}^{\mathrm{2}} +\mathrm{2v}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{4v}^{\mathrm{2}} \right)\right) \\ $$$$\:\:\:\:\:\:\:=\mathrm{3e}^{\mathrm{2u}^{\mathrm{3}} \mathrm{v}^{\mathrm{2}} +\mathrm{8uv}^{\mathrm{4}} } \left(\mathrm{6u}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} −\mathrm{8v}^{\mathrm{4}} \right) \\ $$$$−−−−−−−−−−−−−−−− \\ $$$$\mathrm{ln}\frac{\mathrm{w}}{\mathrm{3}}=\mathrm{xyz}=\mathrm{2uv}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{4v}^{\mathrm{2}} \right)=\mathrm{2u}^{\mathrm{3}} \mathrm{v}^{\mathrm{2}} −\mathrm{8uv}^{\mathrm{4}} \\ $$$$\frac{\mathrm{d}}{\mathrm{du}}\left(\mathrm{ln}\frac{\mathrm{w}}{\mathrm{3}}\right)=\frac{\mathrm{d}}{\mathrm{du}}\left(\mathrm{2u}^{\mathrm{3}} \mathrm{v}^{\mathrm{2}} −\mathrm{8uv}^{\mathrm{4}} \right) \\ $$$$\Rightarrow\frac{\mathrm{w}'}{\mathrm{w}}=\mathrm{6u}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} −\mathrm{8v}^{\mathrm{4}} \\ $$$$\Rightarrow\frac{\partial\mathrm{w}}{\partial\mathrm{u}}=\mathrm{w}\centerdot\left(\mathrm{6u}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} −\mathrm{8v}^{\mathrm{4}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}\left(\mathrm{6u}^{\mathrm{2}} \mathrm{v}^{\mathrm{2}} −\mathrm{8v}^{\mathrm{4}} \right)\centerdot\mathrm{e}^{\mathrm{2u}^{\mathrm{3}} \mathrm{v}^{\mathrm{2}} +\mathrm{8uv}^{\mathrm{4}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply