Question Number 142882 by mohammad17 last updated on 06/Jun/21

Commented by mr W last updated on 06/Jun/21
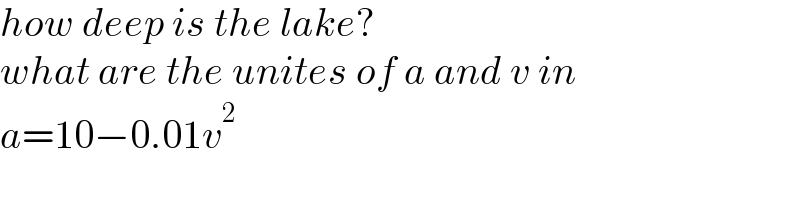
$${how}\:{deep}\:{is}\:{the}\:{lake}? \\ $$$${what}\:{are}\:{the}\:{unites}\:{of}\:{a}\:{and}\:{v}\:{in} \\ $$$${a}=\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} \\ $$
Answered by Olaf_Thorendsen last updated on 07/Jun/21
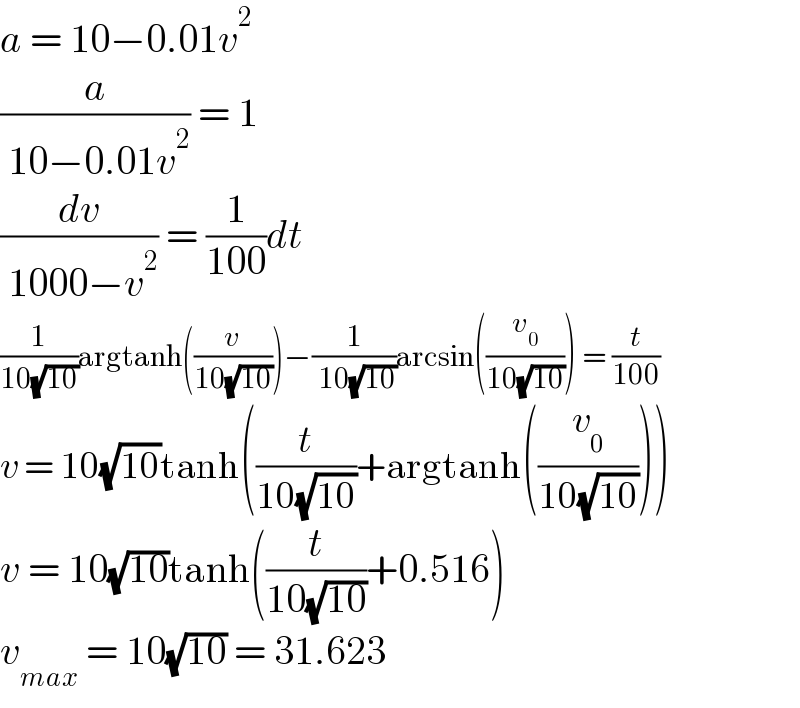
$${a}\:=\:\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} \\ $$$$\frac{{a}}{\:\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$\frac{{dv}}{\:\mathrm{1000}−{v}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{100}}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{10}\sqrt{\mathrm{10}}}\mathrm{argtanh}\left(\frac{{v}}{\mathrm{10}\sqrt{\mathrm{10}}}\right)−\frac{\mathrm{1}}{\:\mathrm{10}\sqrt{\mathrm{10}}}\mathrm{arcsin}\left(\frac{{v}_{\mathrm{0}} }{\mathrm{10}\sqrt{\mathrm{10}}}\right)\:=\:\frac{{t}}{\mathrm{100}} \\ $$$${v}\:=\:\mathrm{10}\sqrt{\mathrm{10}}\mathrm{tanh}\left(\frac{{t}}{\mathrm{10}\sqrt{\mathrm{10}}}+\mathrm{argtanh}\left(\frac{{v}_{\mathrm{0}} }{\mathrm{10}\sqrt{\mathrm{10}}}\right)\right) \\ $$$${v}\:=\:\mathrm{10}\sqrt{\mathrm{10}}\mathrm{tanh}\left(\frac{{t}}{\mathrm{10}\sqrt{\mathrm{10}}}+\mathrm{0}.\mathrm{516}\right) \\ $$$${v}_{{max}} \:=\:\mathrm{10}\sqrt{\mathrm{10}}\:=\:\mathrm{31}.\mathrm{623} \\ $$
Answered by mr W last updated on 07/Jun/21
![a=(dv/dt)=v(dv/dy)=10−0.01v^2 ((vdv)/(10−0.01v^2 ))=dy ∫_v_0 ^v ((vdv)/(10−0.01v^2 ))=∫_0 ^y dy ∫_v_0 ^v ((d(10−0.01v^2 ))/(10−0.01v^2 ))=−0.02∫_0 ^y dy ln ((10−0.01v^2 )/(10−0.01v_0 ^2 ))=−0.02y ((10−0.01v^2 )/(10−0.01v_0 ^2 ))=e^(−0.02y) v^2 =(1/(0.01))[10−(10−0.01v_0 ^2 )e^(−0.02y) ] v=10(√(10−(10−0.01v_0 ^2 )e^(−0.02y) ))](https://www.tinkutara.com/question/Q142959.png)
$${a}=\frac{{dv}}{{dt}}={v}\frac{{dv}}{{dy}}=\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} \\ $$$$\frac{{vdv}}{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} }={dy} \\ $$$$\int_{{v}_{\mathrm{0}} } ^{{v}} \frac{{vdv}}{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{{y}} {dy} \\ $$$$\int_{{v}_{\mathrm{0}} } ^{{v}} \frac{{d}\left(\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} \right)}{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} }=−\mathrm{0}.\mathrm{02}\int_{\mathrm{0}} ^{{y}} {dy} \\ $$$$\mathrm{ln}\:\frac{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} }{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}_{\mathrm{0}} ^{\mathrm{2}} }=−\mathrm{0}.\mathrm{02}{y} \\ $$$$\frac{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}^{\mathrm{2}} }{\mathrm{10}−\mathrm{0}.\mathrm{01}{v}_{\mathrm{0}} ^{\mathrm{2}} }={e}^{−\mathrm{0}.\mathrm{02}{y}} \\ $$$${v}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{0}.\mathrm{01}}\left[\mathrm{10}−\left(\mathrm{10}−\mathrm{0}.\mathrm{01}{v}_{\mathrm{0}} ^{\mathrm{2}} \right){e}^{−\mathrm{0}.\mathrm{02}{y}} \right] \\ $$$${v}=\mathrm{10}\sqrt{\mathrm{10}−\left(\mathrm{10}−\mathrm{0}.\mathrm{01}{v}_{\mathrm{0}} ^{\mathrm{2}} \right){e}^{−\mathrm{0}.\mathrm{02}{y}} } \\ $$
