Question-142900

Question Number 142900 by aliibrahim1 last updated on 06/Jun/21

Commented by qaz last updated on 07/Jun/21

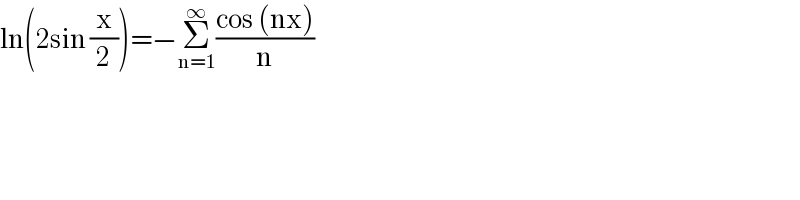
ln(2sin (x/2))=−Σ_(n=1) ^∞ ((cos (nx))/n)

$$\mathrm{ln}\left(\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)=−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{cos}\:\left(\mathrm{nx}\right)}{\mathrm{n}} \\ $$

Commented by mathmax by abdo last updated on 07/Jun/21

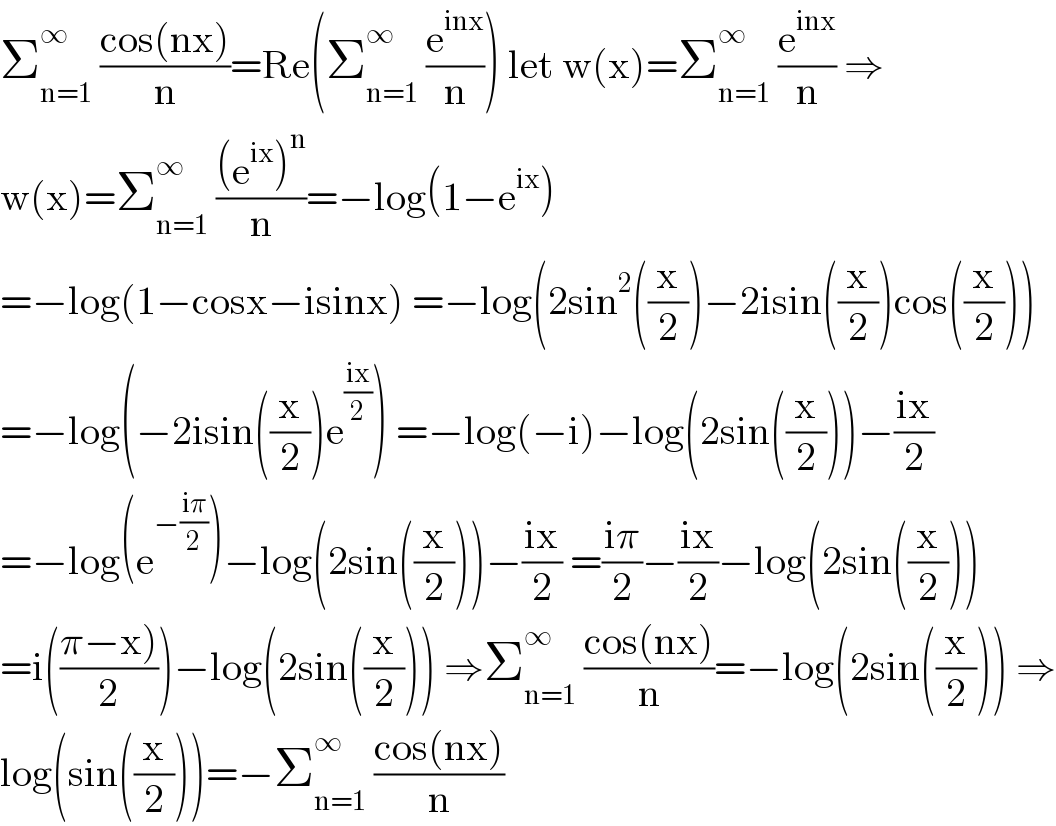
Σ_(n=1) ^∞ ((cos(nx))/n)=Re(Σ_(n=1) ^∞ (e^(inx) /n)) let w(x)=Σ_(n=1) ^∞ (e^(inx) /n) ⇒ w(x)=Σ_(n=1) ^∞ (((e^(ix) )^n )/n)=−log(1−e^(ix) ) =−log(1−cosx−isinx) =−log(2sin^2 ((x/2))−2isin((x/2))cos((x/2))) =−log(−2isin((x/2))e^((ix)/2) ) =−log(−i)−log(2sin((x/2)))−((ix)/2) =−log(e^(−((iπ)/2)) )−log(2sin((x/2)))−((ix)/2) =((iπ)/2)−((ix)/2)−log(2sin((x/2))) =i(((π−x))/2))−log(2sin((x/2))) ⇒Σ_(n=1) ^∞ ((cos(nx))/n)=−log(2sin((x/2))) ⇒ log(sin((x/2)))=−Σ_(n=1) ^∞ ((cos(nx))/n)

$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{n}}=\mathrm{Re}\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{inx}} }{\mathrm{n}}\right)\:\mathrm{let}\:\mathrm{w}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{inx}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\mathrm{w}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{n}} }{\mathrm{n}}=−\mathrm{log}\left(\mathrm{1}−\mathrm{e}^{\mathrm{ix}} \right) \\ $$$$=−\mathrm{log}\left(\mathrm{1}−\mathrm{cosx}−\mathrm{isinx}\right)\:=−\mathrm{log}\left(\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right) \\ $$$$=−\mathrm{log}\left(−\mathrm{2isin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{e}^{\frac{\mathrm{ix}}{\mathrm{2}}} \right)\:=−\mathrm{log}\left(−\mathrm{i}\right)−\mathrm{log}\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)−\frac{\mathrm{ix}}{\mathrm{2}} \\ $$$$=−\mathrm{log}\left(\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{2}}} \right)−\mathrm{log}\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)−\frac{\mathrm{ix}}{\mathrm{2}}\:=\frac{\mathrm{i}\pi}{\mathrm{2}}−\frac{\mathrm{ix}}{\mathrm{2}}−\mathrm{log}\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right) \\ $$$$=\mathrm{i}\left(\frac{\left.\pi−\mathrm{x}\right)}{\mathrm{2}}\right)−\mathrm{log}\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{n}}=−\mathrm{log}\left(\mathrm{2sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\:\Rightarrow \\ $$$$\mathrm{log}\left(\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{nx}\right)}{\mathrm{n}} \\ $$

Commented by aliibrahim1 last updated on 19/Jun/21

$${sorry}\:{took}\:{me}\:{awhile}\:{tl}\:{reply}\:{i}\:{was}\:{offline}\:{but}\:{thank}\:{you}\:{soo}\:{much}\:{sir}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply