Question Number 142927 by bramlexs22 last updated on 07/Jun/21

Answered by Olaf_Thorendsen last updated on 07/Jun/21
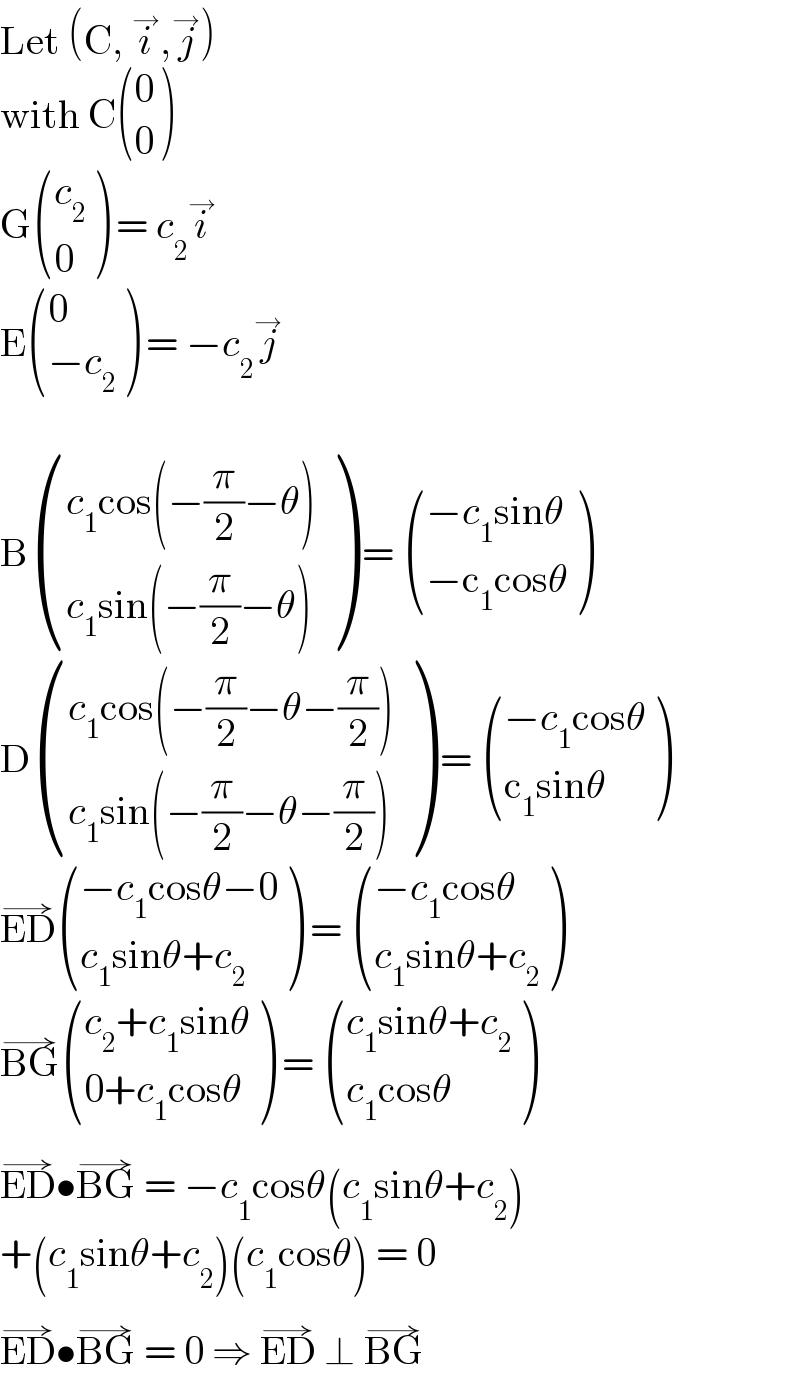
$$\mathrm{Let}\:\left(\mathrm{C},\:\overset{\rightarrow} {{i}},\overset{\rightarrow} {{j}}\right) \\ $$$$\mathrm{with}\:\mathrm{C}\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\mathrm{G}\begin{pmatrix}{{c}_{\mathrm{2}} }\\{\mathrm{0}}\end{pmatrix}\:=\:{c}_{\mathrm{2}} \overset{\rightarrow} {{i}} \\ $$$$\mathrm{E}\begin{pmatrix}{\mathrm{0}}\\{−{c}_{\mathrm{2}} }\end{pmatrix}\:=\:−{c}_{\mathrm{2}} \overset{\rightarrow} {{j}} \\ $$$$ \\ $$$$\mathrm{B}\begin{pmatrix}{{c}_{\mathrm{1}} \mathrm{cos}\left(−\frac{\pi}{\mathrm{2}}−\theta\right)}\\{{c}_{\mathrm{1}} \mathrm{sin}\left(−\frac{\pi}{\mathrm{2}}−\theta\right)}\end{pmatrix}\:=\:\begin{pmatrix}{−{c}_{\mathrm{1}} \mathrm{sin}\theta}\\{−\mathrm{c}_{\mathrm{1}} \mathrm{cos}\theta}\end{pmatrix} \\ $$$$\mathrm{D}\begin{pmatrix}{{c}_{\mathrm{1}} \mathrm{cos}\left(−\frac{\pi}{\mathrm{2}}−\theta−\frac{\pi}{\mathrm{2}}\right)}\\{{c}_{\mathrm{1}} \mathrm{sin}\left(−\frac{\pi}{\mathrm{2}}−\theta−\frac{\pi}{\mathrm{2}}\right)}\end{pmatrix}\:=\:\begin{pmatrix}{−{c}_{\mathrm{1}} \mathrm{cos}\theta}\\{\mathrm{c}_{\mathrm{1}} \mathrm{sin}\theta}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{ED}}\begin{pmatrix}{−{c}_{\mathrm{1}} \mathrm{cos}\theta−\mathrm{0}}\\{{c}_{\mathrm{1}} \mathrm{sin}\theta+{c}_{\mathrm{2}} }\end{pmatrix}\:=\:\begin{pmatrix}{−{c}_{\mathrm{1}} \mathrm{cos}\theta}\\{{c}_{\mathrm{1}} \mathrm{sin}\theta+{c}_{\mathrm{2}} }\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{BG}}\begin{pmatrix}{{c}_{\mathrm{2}} +{c}_{\mathrm{1}} \mathrm{sin}\theta}\\{\mathrm{0}+{c}_{\mathrm{1}} \mathrm{cos}\theta}\end{pmatrix}\:=\:\begin{pmatrix}{{c}_{\mathrm{1}} \mathrm{sin}\theta+{c}_{\mathrm{2}} }\\{{c}_{\mathrm{1}} \mathrm{cos}\theta}\end{pmatrix} \\ $$$$\overset{\rightarrow} {\mathrm{ED}}\bullet\overset{\rightarrow} {\mathrm{BG}}\:=\:−{c}_{\mathrm{1}} \mathrm{cos}\theta\left({c}_{\mathrm{1}} \mathrm{sin}\theta+{c}_{\mathrm{2}} \right) \\ $$$$+\left({c}_{\mathrm{1}} \mathrm{sin}\theta+{c}_{\mathrm{2}} \right)\left({c}_{\mathrm{1}} \mathrm{cos}\theta\right)\:=\:\mathrm{0} \\ $$$$\overset{\rightarrow} {\mathrm{ED}}\bullet\overset{\rightarrow} {\mathrm{BG}}\:=\:\mathrm{0}\:\Rightarrow\:\overset{\rightarrow} {\mathrm{ED}}\:\bot\:\overset{\rightarrow} {\mathrm{BG}} \\ $$
Answered by mr W last updated on 07/Jun/21

Commented by mr W last updated on 07/Jun/21
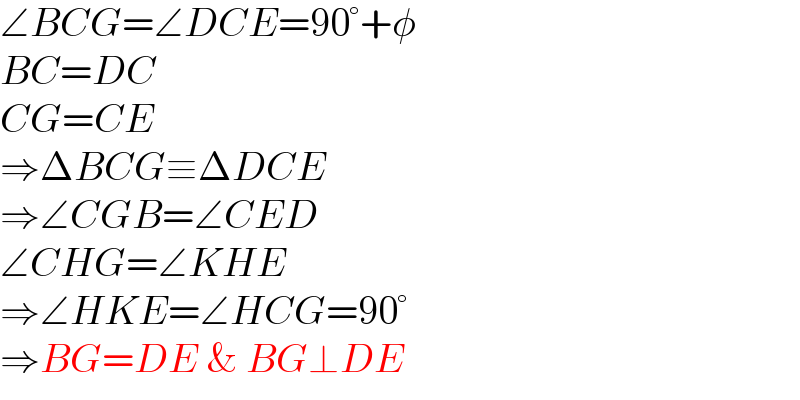
$$\angle{BCG}=\angle{DCE}=\mathrm{90}°+\phi \\ $$$${BC}={DC} \\ $$$${CG}={CE} \\ $$$$\Rightarrow\Delta{BCG}\equiv\Delta{DCE} \\ $$$$\Rightarrow\angle{CGB}=\angle{CED} \\ $$$$\angle{CHG}=\angle{KHE} \\ $$$$\Rightarrow\angle{HKE}=\angle{HCG}=\mathrm{90}° \\ $$$$\Rightarrow{BG}={DE}\:\&\:{BG}\bot{DE} \\ $$
