Question Number 142935 by mnjuly1970 last updated on 07/Jun/21
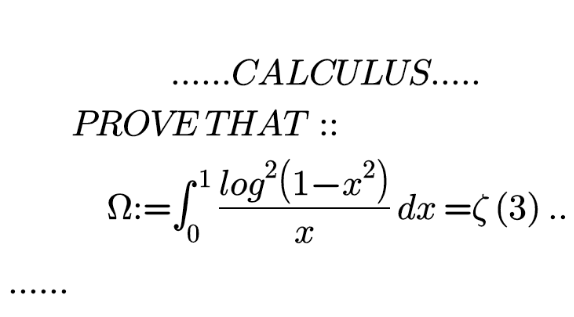
Answered by qaz last updated on 07/Jun/21
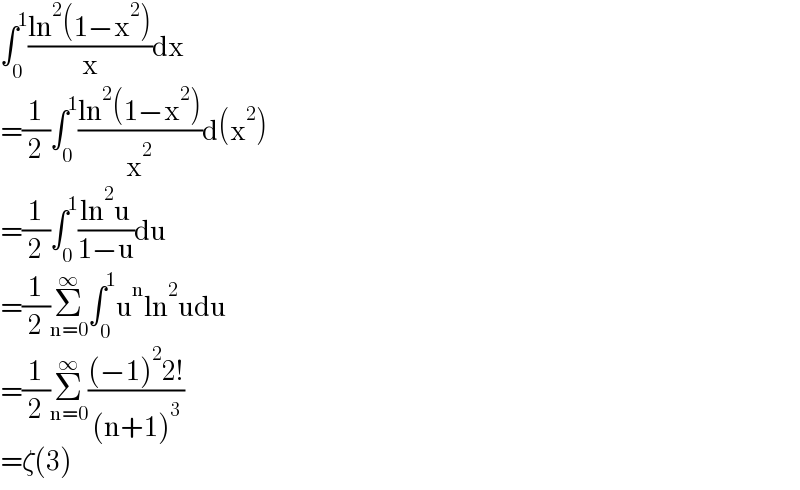
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{u}}{\mathrm{1}−\mathrm{u}}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{u}^{\mathrm{n}} \mathrm{ln}^{\mathrm{2}} \mathrm{udu} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} \mathrm{2}!}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\zeta\left(\mathrm{3}\right) \\ $$
Commented by mnjuly1970 last updated on 07/Jun/21
$$\:{thank}\:{you}\:{very}\:{much}… \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jun/21
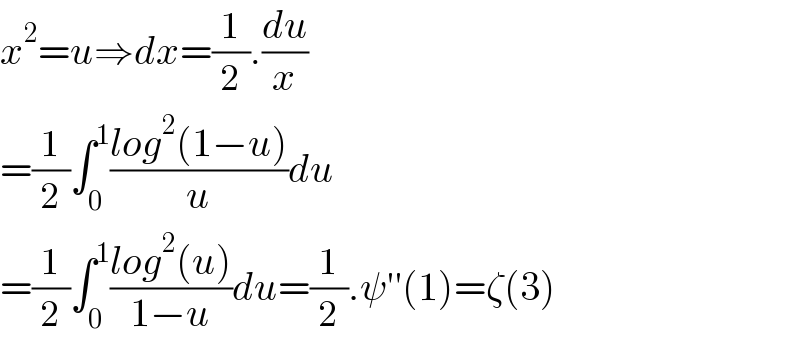
$${x}^{\mathrm{2}} ={u}\Rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{{du}}{{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}^{\mathrm{2}} \left(\mathrm{1}−{u}\right)}{{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}^{\mathrm{2}} \left({u}\right)}{\mathrm{1}−{u}}{du}=\frac{\mathrm{1}}{\mathrm{2}}.\psi''\left(\mathrm{1}\right)=\zeta\left(\mathrm{3}\right) \\ $$
Commented by mnjuly1970 last updated on 07/Jun/21

$$\:\:\:\:\:{thanks}\:{alot}…. \\ $$$$\:\: \\ $$
