Menu Close

Question-142986

Tinku Tara 0 Comments
Pin




Question Number 142986 by mnjuly1970 last updated on 08/Jun/21
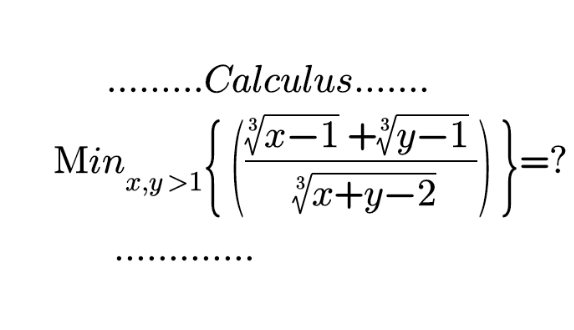
Commented by MJS_new last updated on 08/Jun/21
if y=x the expression is constantly (4)^(1/3)
$$\mathrm{if}\:{y}={x}\:\mathrm{the}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{constantly}\:\:\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 08/Jun/21
perfec...
$${perfec}… \\ $$
Answered by TheHoneyCat last updated on 17/Jun/21
ler c: { (R,→,R),(x,→,x^3 ) :} ∈C^∞ (R) which, by checking the derrivative, is obviously a bijection So: Min_(x,y>1) {((^3 (√(x−1))+^3 (√(y−1)))/(^3 (√(x+y−2))))} =Min_(x,y>0) {((^3 (√x)+^3 (√y))/(^3 (√(x+y))))} _((x⇋x−1, y⇋y−1)) =c^(−1) (Min_(x,y>0) {(((^3 (√x)+^3 (√y))^3 )/(x+y))}) =c^(−1) (Min_(x,y>0) {(((x+y)^3 )/(x^3 +y^3 ))}) _((x⇋^3 (√x), y⇋^3 (√y))) =c^(−1) (Min_(x,y>0) {((x^3 +y^3 +6xy^2 +6yx^2 )/(x^3 +y^3 ))}) =c^(−1) (Min_(x,y>0) {1+6((xy^2 +yx^2 )/(x^3 +y^3 ))}) =c^(−1) (1+6×Min_(x,y>0) {((xy^2 +yx^2 )/(x^3 +y^3 ))}) let (Un)=(1,(1/n))_(n∈N) (Un)∈{x,y ∣ x>0 and y>0} = ′′x,y>0′′ and (((1/n^2 )+(1/n))/(1+(1/n^3 )))→_(n→+∞) 0 So, Min_(x,y>0) {((xy^2 +yx^2 )/(x^3 +y^3 ))}≤0 But ∀(x,y)∈(R_+ ^∗ )^2 ((xy^2 +yx^2 )/(x^3 +y^3 ))}≥0 (∗) So, Min_(x,y>0) {((xy^2 +yx^2 )/(x^3 +y^3 ))}=0 And thus : Min_(x,y>1) {((^3 (√(x−1))+^3 (√(y−1)))/(^3 (√(x+y−2))))}=c^(−1) (1)=1 Your minimum is worth 1 By the way, it is possible to proove that this value cannot be obtained with (x,y)∈(R_+ ^∗ )^2 (∗) is in fact a strict innequality so technically it is not called a Max but a Sup and (∗) would not contradict anything.
$$\mathrm{ler}\:{c}:\begin{cases}{\mathbb{R}}&{\rightarrow}&{\mathbb{R}}\\{{x}}&{\rightarrow}&{{x}^{\mathrm{3}} }\end{cases}\:\in\mathscr{C}^{\infty} \left(\mathbb{R}\right)\:\mathrm{which},\:\mathrm{by}\:\mathrm{checking}\:\mathrm{the}\:\mathrm{derrivative},\:\mathrm{is}\:\mathrm{obviously}\:\mathrm{a}\:\mathrm{bijection} \\ $$$$\mathrm{So}: \\ $$$$\mathrm{Min}_{{x},{y}>\mathrm{1}} \left\{\frac{\:^{\mathrm{3}} \sqrt{{x}−\mathrm{1}}+^{\mathrm{3}} \sqrt{{y}−\mathrm{1}}}{\:^{\mathrm{3}} \sqrt{{x}+{y}−\mathrm{2}}}\right\} \\ $$$$=\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{\:^{\mathrm{3}} \sqrt{{x}}+^{\mathrm{3}} \sqrt{{y}}}{\:^{\mathrm{3}} \sqrt{{x}+{y}}}\right\}\:_{\left({x}\leftrightharpoons{x}−\mathrm{1},\:{y}\leftrightharpoons{y}−\mathrm{1}\right)} \\ $$$$={c}^{−\mathrm{1}} \left(\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{\left(\:^{\mathrm{3}} \sqrt{{x}}+^{\mathrm{3}} \sqrt{{y}}\right)^{\mathrm{3}} }{{x}+{y}}\right\}\right)\: \\ $$$$={c}^{−\mathrm{1}} \left(\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{\left({x}+{y}\right)^{\mathrm{3}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}\right)\:_{\left({x}\leftrightharpoons^{\mathrm{3}} \sqrt{{x}},\:{y}\leftrightharpoons^{\mathrm{3}} \sqrt{{y}}\right)} \\ $$$$={c}^{−\mathrm{1}} \left(\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +\mathrm{6}{xy}^{\mathrm{2}} +\mathrm{6}{yx}^{\mathrm{2}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}\right) \\ $$$$={c}^{−\mathrm{1}} \left(\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\mathrm{1}+\mathrm{6}\frac{{xy}^{\mathrm{2}} +{yx}^{\mathrm{2}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}\right) \\ $$$$={c}^{−\mathrm{1}} \left(\mathrm{1}+\mathrm{6}×\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{{xy}^{\mathrm{2}} +{yx}^{\mathrm{2}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}\right) \\ $$$$ \\ $$$$\mathrm{let}\:\left({Un}\right)=\left(\mathrm{1},\frac{\mathrm{1}}{{n}}\right)_{{n}\in\mathbb{N}} \\ $$$$\left({Un}\right)\in\left\{{x},{y}\:\mid\:{x}>\mathrm{0}\:\mathrm{and}\:{y}>\mathrm{0}\right\}\:=\:''{x},{y}>\mathrm{0}'' \\ $$$$\mathrm{and}\:\frac{\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{{n}}}{\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{3}} }}\underset{{n}\rightarrow+\infty} {\rightarrow}\mathrm{0} \\ $$$$\mathrm{So},\:\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{{xy}^{\mathrm{2}} +{yx}^{\mathrm{2}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}\leqslant\mathrm{0} \\ $$$$\left.\mathrm{But}\:\forall\left({x},{y}\right)\in\left(\mathbb{R}_{+} ^{\ast} \right)^{\mathrm{2}} \:\frac{{xy}^{\mathrm{2}} +{yx}^{\mathrm{2}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}\geqslant\mathrm{0}\:\left(\ast\right) \\ $$$$\mathrm{So},\:\mathrm{Min}_{{x},{y}>\mathrm{0}} \left\{\frac{{xy}^{\mathrm{2}} +{yx}^{\mathrm{2}} }{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }\right\}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{And}\:\mathrm{thus}\:: \\ $$$$\mathrm{Min}_{{x},{y}>\mathrm{1}} \left\{\frac{\:^{\mathrm{3}} \sqrt{{x}−\mathrm{1}}+^{\mathrm{3}} \sqrt{{y}−\mathrm{1}}}{\:^{\mathrm{3}} \sqrt{{x}+{y}−\mathrm{2}}}\right\}={c}^{−\mathrm{1}} \left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{Your}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{worth}\:\mathrm{1} \\ $$$$ \\ $$$${By}\:{the}\:{way},\:{it}\:{is}\:{possible}\:{to}\:{proove}\:{that}\:{this}\:{value}\:{cannot}\:{be}\:{obtained}\:{with}\:\left({x},{y}\right)\in\left(\mathbb{R}_{+} ^{\ast} \right)^{\mathrm{2}} \\ $$$$\left(\ast\right)\:{is}\:{in}\:{fact}\:{a}\:{strict}\:{innequality} \\ $$$${so}\:{technically}\:{it}\:{is}\:{not}\:{called}\:{a}\:{Max}\:{but}\:{a}\:{Sup} \\ $$$${and}\:\left(\ast\right)\:{would}\:{not}\:{contradict}\:{anything}. \\ $$$$ \\ $$
Answered by ajfour last updated on 17/Jun/21
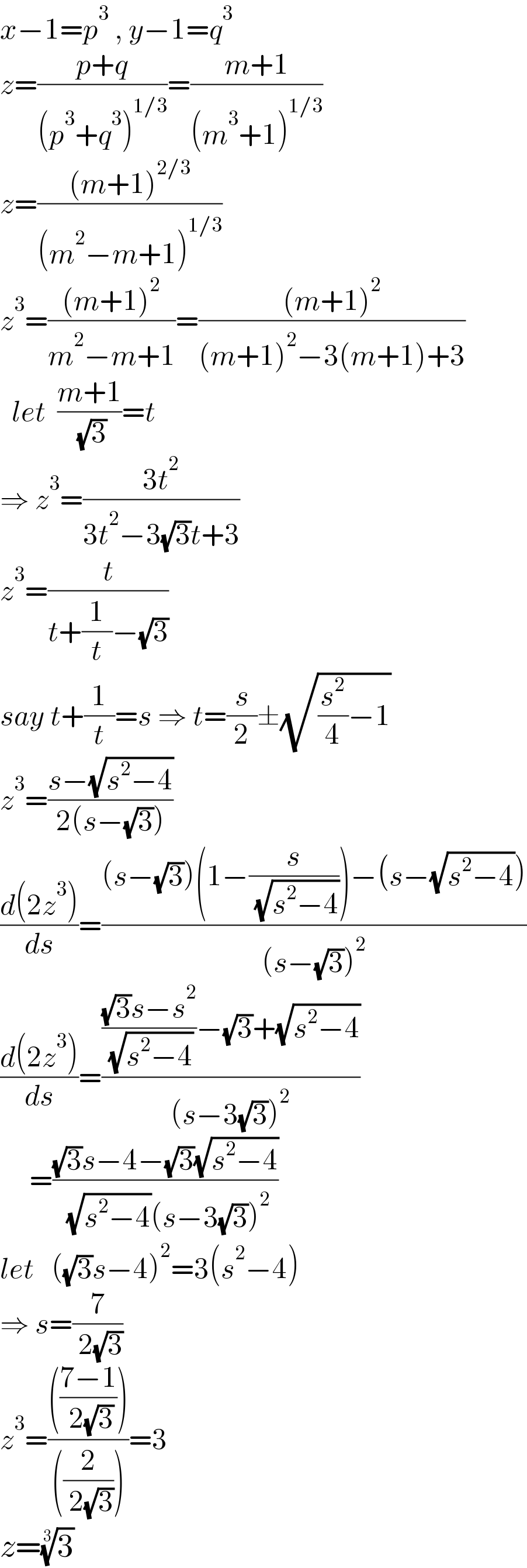
x−1=p^3 , y−1=q^3 z=((p+q)/((p^3 +q^3 )^(1/3) ))=((m+1)/((m^3 +1)^(1/3) )) z=(((m+1)^(2/3) )/((m^2 −m+1)^(1/3) )) z^3 =(((m+1)^2 )/(m^2 −m+1))=(((m+1)^2 )/((m+1)^2 −3(m+1)+3)) let ((m+1)/( (√3)))=t ⇒ z^3 =((3t^2 )/(3t^2 −3(√3)t+3)) z^3 =(t/(t+(1/t)−(√3))) say t+(1/t)=s ⇒ t=(s/2)±(√((s^2 /4)−1)) z^3 =((s−(√(s^2 −4)))/(2(s−(√3)))) ((d(2z^3 ))/ds)=(((s−(√3))(1−(s/( (√(s^2 −4)))))−(s−(√(s^2 −4))))/((s−(√3))^2 )) ((d(2z^3 ))/ds)=(((((√3)s−s^2 )/( (√(s^2 −4))))−(√3)+(√(s^2 −4)))/((s−3(√3))^2 )) =(((√3)s−4−(√3)(√(s^2 −4)))/( (√(s^2 −4))(s−3(√3))^2 )) let ((√3)s−4)^2 =3(s^2 −4) ⇒ s=(7/( 2(√3))) z^3 =(((((7−1)/( 2(√3)))))/(((2/( 2(√3))))))=3 z=(3)^(1/3)
$${x}−\mathrm{1}={p}^{\mathrm{3}} \:,\:{y}−\mathrm{1}={q}^{\mathrm{3}} \\ $$$${z}=\frac{{p}+{q}}{\left({p}^{\mathrm{3}} +{q}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} }=\frac{{m}+\mathrm{1}}{\left({m}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} } \\ $$$${z}=\frac{\left({m}+\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} }{\left({m}^{\mathrm{2}} −{m}+\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} } \\ $$$${z}^{\mathrm{3}} =\frac{\left({m}+\mathrm{1}\right)^{\mathrm{2}} }{{m}^{\mathrm{2}} −{m}+\mathrm{1}}=\frac{\left({m}+\mathrm{1}\right)^{\mathrm{2}} }{\left({m}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{3}\left({m}+\mathrm{1}\right)+\mathrm{3}} \\ $$$$\:\:{let}\:\:\frac{{m}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}={t} \\ $$$$\Rightarrow\:{z}^{\mathrm{3}} =\frac{\mathrm{3}{t}^{\mathrm{2}} }{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{3}\sqrt{\mathrm{3}}{t}+\mathrm{3}} \\ $$$${z}^{\mathrm{3}} =\frac{{t}}{{t}+\frac{\mathrm{1}}{{t}}−\sqrt{\mathrm{3}}} \\ $$$${say}\:{t}+\frac{\mathrm{1}}{{t}}={s}\:\Rightarrow\:{t}=\frac{{s}}{\mathrm{2}}\pm\sqrt{\frac{{s}^{\mathrm{2}} }{\mathrm{4}}−\mathrm{1}} \\ $$$${z}^{\mathrm{3}} =\frac{{s}−\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}\left({s}−\sqrt{\mathrm{3}}\right)} \\ $$$$\frac{{d}\left(\mathrm{2}{z}^{\mathrm{3}} \right)}{{ds}}=\frac{\left({s}−\sqrt{\mathrm{3}}\right)\left(\mathrm{1}−\frac{{s}}{\:\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}}\right)−\left({s}−\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}\right)}{\left({s}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\frac{{d}\left(\mathrm{2}{z}^{\mathrm{3}} \right)}{{ds}}=\frac{\frac{\sqrt{\mathrm{3}}{s}−{s}^{\mathrm{2}} }{\:\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}}−\sqrt{\mathrm{3}}+\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}}{\left({s}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}{s}−\mathrm{4}−\sqrt{\mathrm{3}}\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}}{\:\sqrt{{s}^{\mathrm{2}} −\mathrm{4}}\left({s}−\mathrm{3}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$${let}\:\:\:\left(\sqrt{\mathrm{3}}{s}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{3}\left({s}^{\mathrm{2}} −\mathrm{4}\right) \\ $$$$\Rightarrow\:{s}=\frac{\mathrm{7}}{\:\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$${z}^{\mathrm{3}} =\frac{\left(\frac{\mathrm{7}−\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\right)}{\left(\frac{\mathrm{2}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\right)}=\mathrm{3} \\ $$$${z}=\sqrt[{\mathrm{3}}]{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *