Question Number 143027 by mathlove last updated on 09/Jun/21
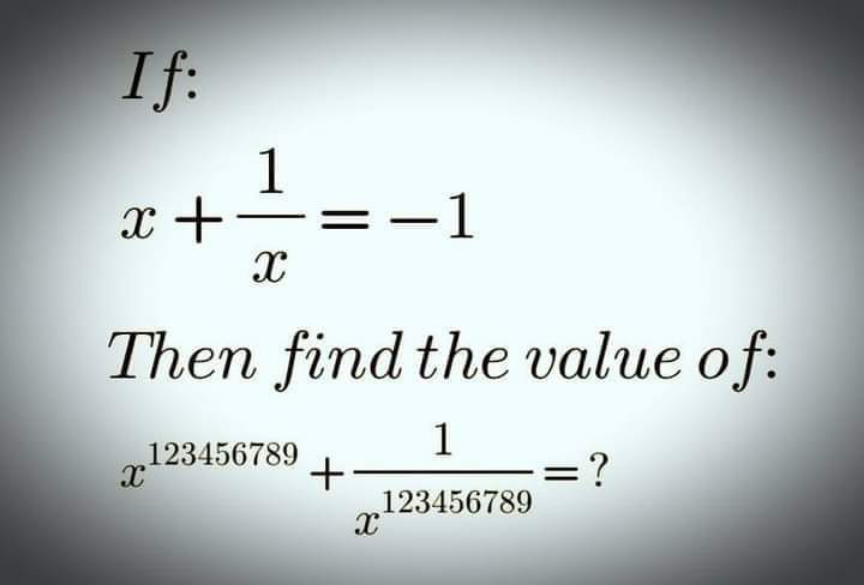
Commented by Rasheed.Sindhi last updated on 09/Jun/21
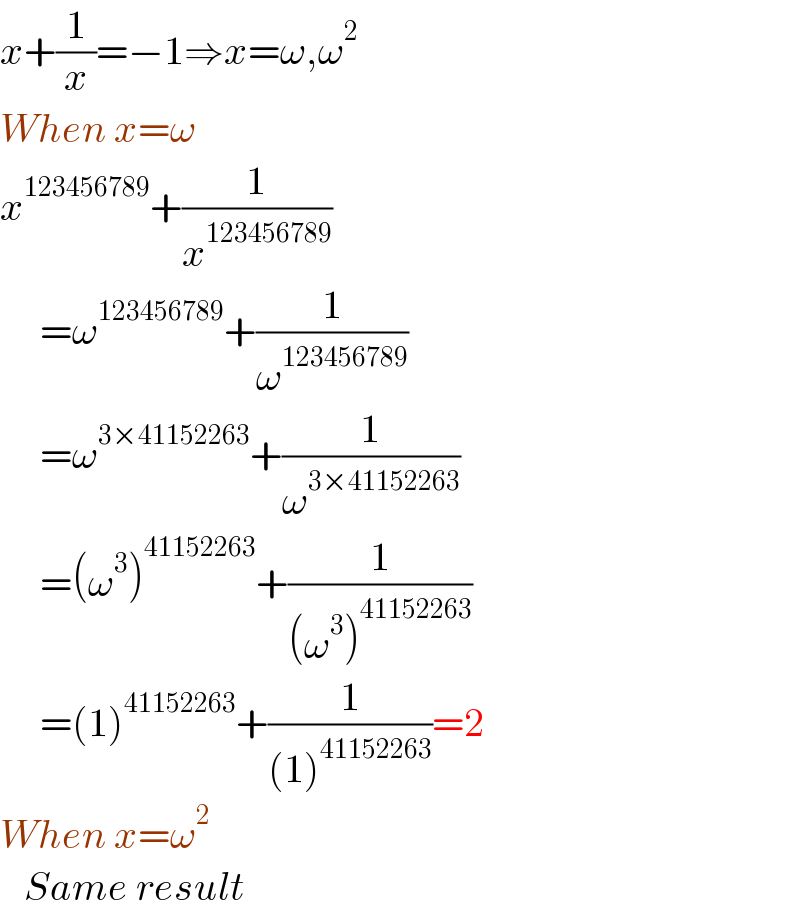
$${x}+\frac{\mathrm{1}}{{x}}=−\mathrm{1}\Rightarrow{x}=\omega,\omega^{\mathrm{2}} \\ $$$${When}\:{x}=\omega \\ $$$${x}^{\mathrm{123456789}} +\frac{\mathrm{1}}{{x}^{\mathrm{123456789}} } \\ $$$$\:\:\:\:\:=\omega^{\mathrm{123456789}} +\frac{\mathrm{1}}{\omega^{\mathrm{123456789}} } \\ $$$$\:\:\:\:\:=\omega^{\mathrm{3}×\mathrm{41152263}} +\frac{\mathrm{1}}{\omega^{\mathrm{3}×\mathrm{41152263}} } \\ $$$$\:\:\:\:\:=\left(\omega^{\mathrm{3}} \right)^{\mathrm{41152263}} +\frac{\mathrm{1}}{\left(\omega^{\mathrm{3}} \right)^{\mathrm{41152263}} } \\ $$$$\:\:\:\:\:=\left(\mathrm{1}\right)^{\mathrm{41152263}} +\frac{\mathrm{1}}{\left(\mathrm{1}\right)^{\mathrm{41152263}} }=\mathrm{2} \\ $$$${When}\:{x}=\omega^{\mathrm{2}} \\ $$$$\:\:\:{Same}\:{result} \\ $$
Answered by mathmax by abdo last updated on 09/Jun/21
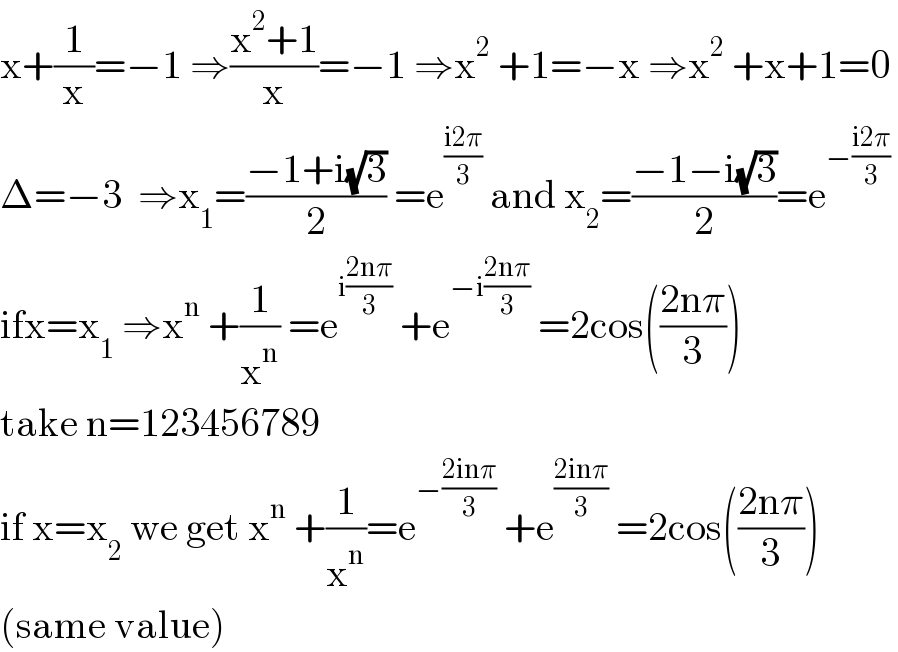
$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}=−\mathrm{1}\:\Rightarrow\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{x}}=−\mathrm{1}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}=−\mathrm{x}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Delta=−\mathrm{3}\:\:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \: \\ $$$$\mathrm{ifx}=\mathrm{x}_{\mathrm{1}} \:\Rightarrow\mathrm{x}^{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }\:=\mathrm{e}^{\mathrm{i}\frac{\mathrm{2n}\pi}{\mathrm{3}}} \:+\mathrm{e}^{−\mathrm{i}\frac{\mathrm{2n}\pi}{\mathrm{3}}} \:=\mathrm{2cos}\left(\frac{\mathrm{2n}\pi}{\mathrm{3}}\right) \\ $$$$\mathrm{take}\:\mathrm{n}=\mathrm{123456789} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{x}_{\mathrm{2}} \:\mathrm{we}\:\mathrm{get}\:\mathrm{x}^{\mathrm{n}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{n}} }=\mathrm{e}^{−\frac{\mathrm{2in}\pi}{\mathrm{3}}} \:+\mathrm{e}^{\frac{\mathrm{2in}\pi}{\mathrm{3}}} \:=\mathrm{2cos}\left(\frac{\mathrm{2n}\pi}{\mathrm{3}}\right) \\ $$$$\left(\mathrm{same}\:\mathrm{value}\right) \\ $$
