Menu Close

Question-143127

Tinku Tara 0 Comments
Pin




Question Number 143127 by liberty last updated on 10/Jun/21
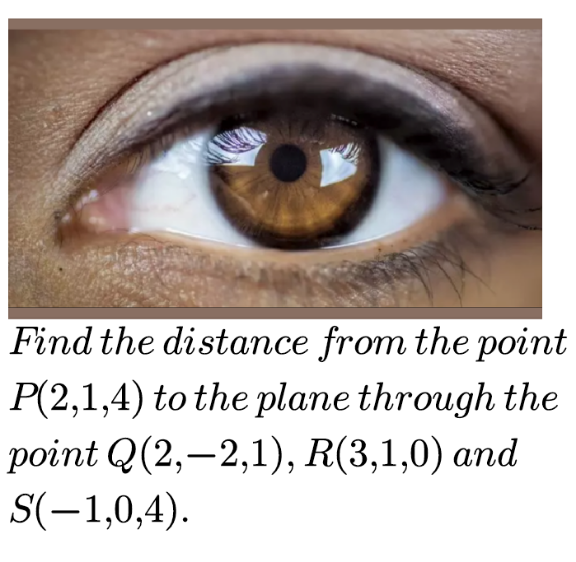
Answered by EDWIN88 last updated on 11/Jun/21
Let { ((a^→ =QR=(1,3,−1))),((b^→ =QS=(−3,2,3))),((c^→ =QP=(0,3,3))) :} distance d from P to plane is d = ((∣a^→ .(b^→ ×c^→ )∣)/(∣a^→ ×b^→ ∣)) (1)a^→ .(b^→ ×c^→ )= determinant ((( 1 3 −1 )),((−3 2 3 )),(( 0 3 3))) = 1(−3)−3(−9)−1(−9) = −3+27+9 = 33 (2) a^→ ×b^→ = determinant ((( 1 3 −1)),((−3 2 3))) = (11,0,11) ⇒ distance = ((33)/( (√(121+121)))) = ((33)/(11(√2))) = (3/( (√2))) ⇒distance = (3/( (√2))) □
$$\:\mathrm{Let}\:\begin{cases}{\overset{\rightarrow} {\mathrm{a}}=\mathrm{QR}=\left(\mathrm{1},\mathrm{3},−\mathrm{1}\right)}\\{\overset{\rightarrow} {\mathrm{b}}=\mathrm{QS}=\left(−\mathrm{3},\mathrm{2},\mathrm{3}\right)}\\{\overset{\rightarrow} {\mathrm{c}}=\mathrm{QP}=\left(\mathrm{0},\mathrm{3},\mathrm{3}\right)}\end{cases} \\ $$$$\mathrm{distance}\:\mathrm{d}\:\mathrm{from}\:\mathrm{P}\:\mathrm{to}\:\mathrm{plane}\:\mathrm{is}\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{d}\:=\:\frac{\mid\overset{\rightarrow} {\mathrm{a}}.\left(\overset{\rightarrow} {\mathrm{b}}×\overset{\rightarrow} {\mathrm{c}}\right)\mid}{\mid\overset{\rightarrow} {\mathrm{a}}×\overset{\rightarrow} {\mathrm{b}}\mid} \\ $$$$\left(\mathrm{1}\right)\overset{\rightarrow} {\mathrm{a}}.\left(\overset{\rightarrow} {\mathrm{b}}×\overset{\rightarrow} {\mathrm{c}}\right)=\begin{vmatrix}{\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:−\mathrm{1}\:}\\{−\mathrm{3}\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{3}\:}\\{\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}\left(−\mathrm{3}\right)−\mathrm{3}\left(−\mathrm{9}\right)−\mathrm{1}\left(−\mathrm{9}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{3}+\mathrm{27}+\mathrm{9}\:=\:\mathrm{33} \\ $$$$\left(\mathrm{2}\right)\:\overset{\rightarrow} {\mathrm{a}}×\overset{\rightarrow} {\mathrm{b}}\:=\:\begin{vmatrix}{\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{3}\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{3}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{11},\mathrm{0},\mathrm{11}\right) \\ $$$$\Rightarrow\:\mathrm{distance}\:=\:\frac{\mathrm{33}}{\:\sqrt{\mathrm{121}+\mathrm{121}}}\:=\:\frac{\mathrm{33}}{\mathrm{11}\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{distance}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\:\Box\: \\ $$
Commented by EDWIN88 last updated on 11/Jun/21
wrong. it should be d = ((∣b^→ .(c^→ ×a^→ )∣)/(∣b^→ ×c^→ ∣)) where b^→ .(c^→ ×a^→ )= determinant ((( 1 3 −1)),((−3 2 3)),(( 0 3 3))) = 1(−3)−3(−9)−1(−9) = −3+27+9 = 33 and b^→ ×c^→ = determinant ((( 1 3 −1)),((−3 2 3))) = (11,0,11) therefore d = ((33)/( (√(121+121)))) = ((33)/(11(√2))) = (3/( (√2)))
$$\mathrm{wrong}. \\ $$$$\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{d}\:=\:\frac{\mid\overset{\rightarrow} {\mathrm{b}}.\left(\overset{\rightarrow} {\mathrm{c}}×\overset{\rightarrow} {\mathrm{a}}\right)\mid}{\mid\overset{\rightarrow} {\mathrm{b}}×\overset{\rightarrow} {\mathrm{c}}\mid} \\ $$$$\mathrm{where}\:\overset{\rightarrow} {\mathrm{b}}.\left(\overset{\rightarrow} {\mathrm{c}}×\overset{\rightarrow} {\mathrm{a}}\right)=\:\begin{vmatrix}{\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{3}\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\\{\:\:\:\:\mathrm{0}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}\left(−\mathrm{3}\right)−\mathrm{3}\left(−\mathrm{9}\right)−\mathrm{1}\left(−\mathrm{9}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:−\mathrm{3}+\mathrm{27}+\mathrm{9}\:=\:\mathrm{33} \\ $$$$\mathrm{and}\:\overset{\rightarrow} {\mathrm{b}}×\overset{\rightarrow} {\mathrm{c}}=\:\begin{vmatrix}{\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{3}\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{3}\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{11},\mathrm{0},\mathrm{11}\right) \\ $$$$\mathrm{therefore}\:\mathrm{d}\:=\:\frac{\mathrm{33}}{\:\sqrt{\mathrm{121}+\mathrm{121}}}\:=\:\frac{\mathrm{33}}{\mathrm{11}\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by liberty last updated on 10/Jun/21
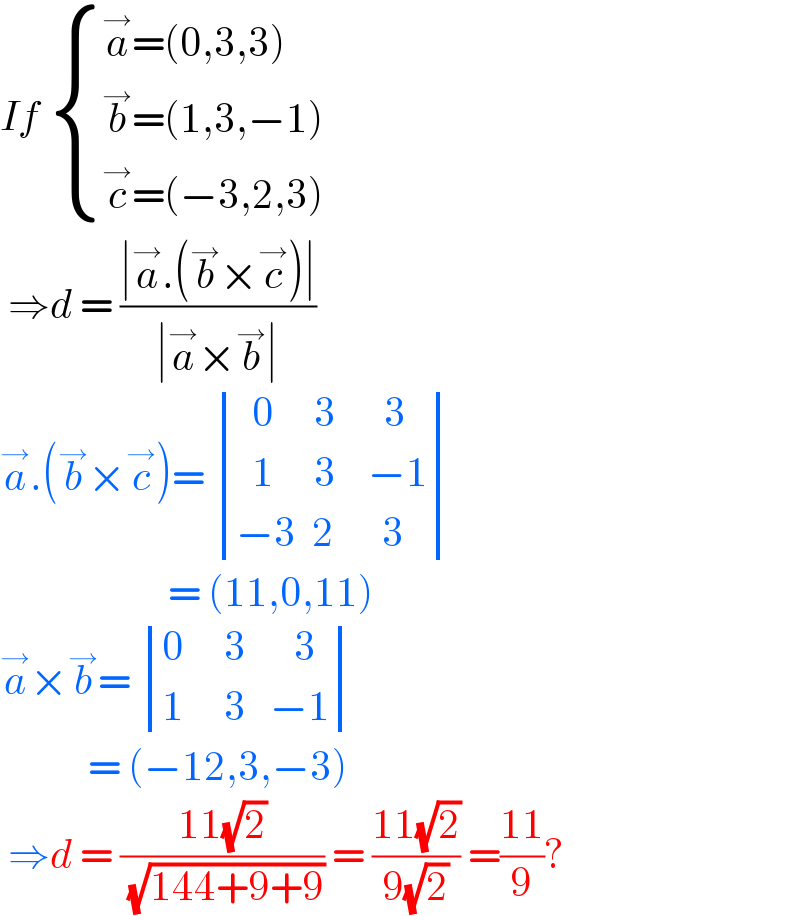
If { ((a^→ =(0,3,3))),((b^→ =(1,3,−1))),((c^→ =(−3,2,3))) :} ⇒d = ((∣a^→ .(b^→ ×c^→ )∣)/(∣a^→ ×b^→ ∣)) a^→ .(b^→ ×c^→ )= determinant ((( 0 3 3)),(( 1 3 −1)),((−3 2 3))) = (11,0,11) a^→ ×b^→ = determinant (((0 3 3)),((1 3 −1))) = (−12,3,−3) ⇒d = ((11(√2))/( (√(144+9+9)))) = ((11(√2))/(9(√2))) =((11)/9)?
$${If}\:\begin{cases}{\overset{\rightarrow} {{a}}=\left(\mathrm{0},\mathrm{3},\mathrm{3}\right)}\\{\overset{\rightarrow} {{b}}=\left(\mathrm{1},\mathrm{3},−\mathrm{1}\right)}\\{\overset{\rightarrow} {{c}}=\left(−\mathrm{3},\mathrm{2},\mathrm{3}\right)}\end{cases} \\ $$$$\:\Rightarrow{d}\:=\:\frac{\mid\overset{\rightarrow} {{a}}.\left(\overset{\rightarrow} {{b}}×\overset{\rightarrow} {{c}}\right)\mid}{\mid\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\mid} \\ $$$$\overset{\rightarrow} {{a}}.\left(\overset{\rightarrow} {{b}}×\overset{\rightarrow} {{c}}\right)=\:\begin{vmatrix}{\:\:\mathrm{0}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{3}}\\{\:\:\mathrm{1}\:\:\:\:\:\mathrm{3}\:\:\:\:−\mathrm{1}}\\{−\mathrm{3}\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{3}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{11},\mathrm{0},\mathrm{11}\right) \\ $$$$\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}=\:\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{3}}\\{\mathrm{1}\:\:\:\:\:\mathrm{3}\:\:\:−\mathrm{1}}\end{vmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\left(−\mathrm{12},\mathrm{3},−\mathrm{3}\right) \\ $$$$\:\Rightarrow{d}\:=\:\frac{\mathrm{11}\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{144}+\mathrm{9}+\mathrm{9}}}\:=\:\frac{\mathrm{11}\sqrt{\mathrm{2}}}{\mathrm{9}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{11}}{\mathrm{9}}? \\ $$
Answered by mr W last updated on 11/Jun/21
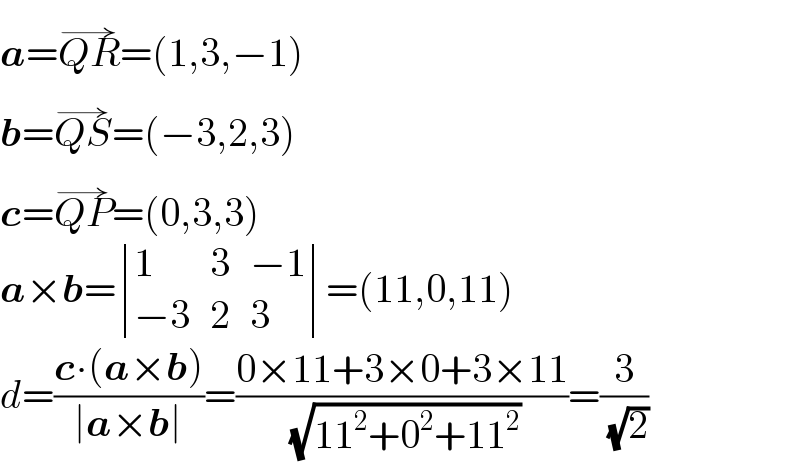
a=QR^(→) =(1,3,−1) b=QS^(→) =(−3,2,3) c=QP^(→) =(0,3,3) a×b= determinant ((1,3,(−1)),((−3),2,3))=(11,0,11) d=((c∙(a×b))/(∣a×b∣))=((0×11+3×0+3×11)/( (√(11^2 +0^2 +11^2 ))))=(3/( (√2)))
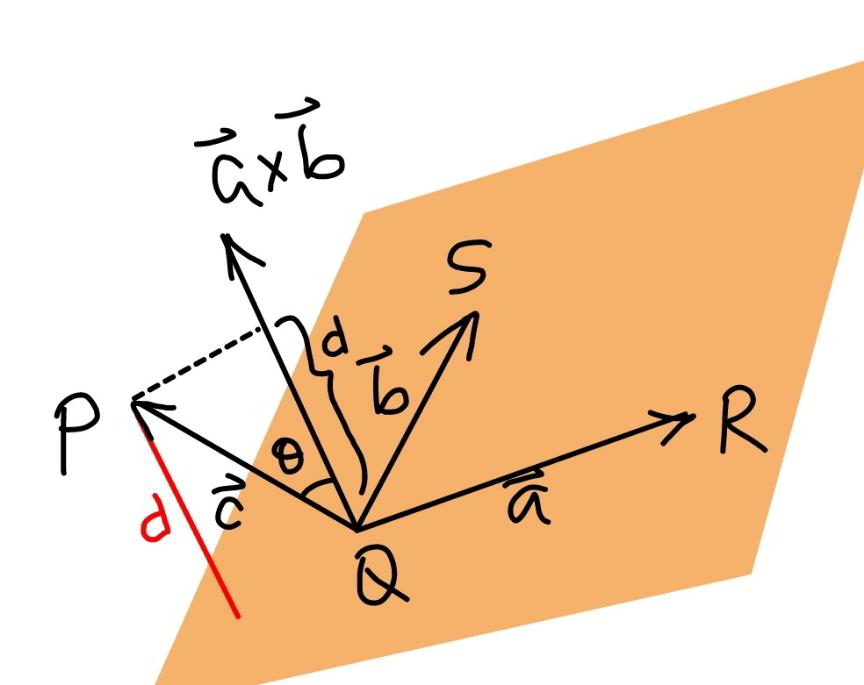
$$\boldsymbol{{a}}=\overset{\rightarrow} {{QR}}=\left(\mathrm{1},\mathrm{3},−\mathrm{1}\right) \\ $$$$\boldsymbol{{b}}=\overset{\rightarrow} {{QS}}=\left(−\mathrm{3},\mathrm{2},\mathrm{3}\right) \\ $$$$\boldsymbol{{c}}=\overset{\rightarrow} {{QP}}=\left(\mathrm{0},\mathrm{3},\mathrm{3}\right) \\ $$$$\boldsymbol{{a}}×\boldsymbol{{b}}=\begin{vmatrix}{\mathrm{1}}&{\mathrm{3}}&{−\mathrm{1}}\\{−\mathrm{3}}&{\mathrm{2}}&{\mathrm{3}}\end{vmatrix}=\left(\mathrm{11},\mathrm{0},\mathrm{11}\right) \\ $$$${d}=\frac{\boldsymbol{{c}}\centerdot\left(\boldsymbol{{a}}×\boldsymbol{{b}}\right)}{\mid\boldsymbol{{a}}×\boldsymbol{{b}}\mid}=\frac{\mathrm{0}×\mathrm{11}+\mathrm{3}×\mathrm{0}+\mathrm{3}×\mathrm{11}}{\:\sqrt{\mathrm{11}^{\mathrm{2}} +\mathrm{0}^{\mathrm{2}} +\mathrm{11}^{\mathrm{2}} }}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by mr W last updated on 10/Jun/21

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *